I am not bound to please thee with my answers.
— SHYLOCK, in The Merchant of Venice (Act IV, Scene 1, Line 65)
1. An average problem for a mathematically inclined reader.
4. See W. J. LeVeque, Topics in Number Theory 2 (Reading, Mass.: Addison–Wesley, 1956), Chapter 3; P. Ribenboim, 13 Lectures on Fermat’s Last Theorem (New York: Springer-Verlag, 1979); A. Wiles, Annals of Mathematics (2) 141 (1995), 443–551.
1. $t←a$, $a←b$, $b←c$, $c←d$, $d←t$.
2. After the first time, the values of the variables m and n are the previous values of n and r, respectively; and $n\gt r$.
3. Algorithm F (Euclid’s algorithm). Given two positive integers m and n, find their greatest common divisor.
F1. [Remainder $m/n$.] Divide m by n and let m be the remainder.
F2. [Is it zero?] If $m=0$, the algorithm terminates with answer n.
F3. [Remainder $n/m$.] Divide n by m and let n be the remainder.
F4. [Is it zero?] If $n=0$, the algorithm terminates with answer m; otherwise go back to step F1. 
4. By Algorithm E, n = 6099, 2166, 1767, 399, 171, 57. Answer: 57.
5. Not finite nor definite nor effective, perhaps no output; in format, no letter is given before step numbers, no summary phrase appears, and there is no “  ”.
”.
6. Trying Algorithm E with n = 5 and m = 1, 2, 3, 4, 5, we find that step E1 is executed 2, 3, 4, 3, 1 times, respectively. So the average is $2.6=T_{5}$.
7. In all but a finite number of cases, $n\gt m$. And when $n\gt m$, the first iteration of Algorithm E merely exchanges these numbers; so $U_{m}=T_{m}+1$.
8. Let $A=\{a,b,c\}$, $N=5$. The algorithm will terminate with the string $a^{\gcd(m,n)}$.

Each iteration either decreases m or keeps m unchanged and decreases n.
9. For example we can say $C_{2}$ represents $C_{1}$ if there is a function g from $I_{1}$ into $I_{2}$, a function h from $Q_{2}$ into $Q_{1}$, and a function j from $Q_{2}$ into the positive integers, satisfying the following conditions:
a) If x is in $I_{1}$ then $h(g(x))=x$.
b) If q is in $Q_{2}$ then $f_{1}(h(q))=h(f_{2}^{[j(q)]}(q))$, where $f_{2}^{[j(q)]}$ means that the function $f_{2}$ is to be iterated $j(q)$ times.
c) If q is in $Q_{2}$ then $h(q)$ is in $Ω_{1}$ if and only if q is in $Ω_{2}$.
For example, let $C_{1}$ be as in (2) and let $C_{2}$ have $I_{2}=\{(m,n)\}$, $Ω_{2}=\{(m,n,d)\}$, $Q_{2}=I_{2}∪Ω_{2}∪\{(m,n,a,b,1)\}∪$ $\{(m,n,a,b,r,2)\}∪\{(m,n,a,b,r,3)\}∪$ $\{(m,n,a,b,r,4)\}∪\{(m,n,a,b,5)\}$. Let $f_{2}((m,n))=(m,n,m,n,1)$; $f_{2}((m,n,d))=(m,n,d)$; $f_{2}((m,n,a,b,1))=(m,n,a,b,a\bmod b,2)$; $f_{2}((m,n,a,b,r,2))=(m,n,b)$ if r = 0, otherwise $(m,n,a,b,r,3)$; $f_{2}((m,n,a,b,r,3))=(m,n,b,b,r,4)$; $f_{2}((m,n,a,b,r,4))=(m,n,a,r,5)$; $f_{2}((m,n,a,b,5))=f_{2}((m,n,a,b,1))$.
Now let $h((m,n))=g((m,n))=(m,n)$; $h((m,n,d))=(d)$; $h((m,n,a,b,1))=(a,b,0,1)$; $h((m,n,a,b,r,2))=(a,b,r,2)$; $h((m,n,a,b,r,3))=(a,b,r,3)$; $h((m,n,a,b,r,4))=h(f_{2}((m,n,a,b,r,4)))$; $h((m,n,a,b,5))=(a,b,b,1)$; $j((m,n,a,b,r,3))=j((m,n,a,b,r,4))=2$, otherwise $j(q)=1$. Then $C_{2}$ represents $C_{1}$.
Notes: It is tempting to try to define things in a more simple way—for example, to let g map $Q_{1}$ into $Q_{2}$ and to insist only that when $x_{0},x_{1},\ldots$ is a computational sequence in $C_{1}$ then $g(x_{0}),g(x_{1}),\ldots$ is a subsequence of the computational sequence in $C_{2}$ that begins with $g(x_{0})$. But this is inadequate; in the example above, $C_{1}$ forgets the original value of m and n but $C_{2}$ does not.
If $C_{2}$ represents $C_{1}$ by means of functions g, h, j, and if $C_{3}$ represents $C_{2}$ by means of functions g′, h′, j′, then $C_{3}$ represents $C_{1}$ by means of functions $g''$, $h''$, $j''$, where
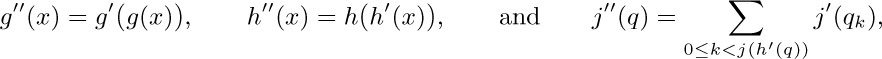
if $q_{0}=q$ and $q_{k+1}=f_{3}^{\large[j'(q_{k})]}(q_k)$. Hence the relation defined above is transitive. We can say $C_{2}$ directly represents $C_{1}$ if the function j is bounded; this relation is also transitive. The relation “$C_{2}$ represents $C_{1}$” generates an equivalence relation in which two computational methods apparently are equivalent if and only if they compute isomorphic functions of their inputs; the relation “$C_{2}$ directly represents $C_{1}$” generates a more interesting equivalence relation that perhaps matches the intuitive idea of being “essentially the same algorithm.”
For an alternative approach to simulation, see R. W. Floyd and R. Beigel, The Language of Machines (Computer Science Press, 1994), Section 3.3.
1. (a) Prove $P(0)$. (b) Prove that $P(0),\ldots,P(n)$ implies $P(n+1)$, for all $n≥0$.
2. The theorem has not been proved for $n=2$. In the second part of the proof, take $n=1$; we assume there that $a^{(n-1)-1}=a^{-1}=1$. If this condition is true (so that $a=1$), the theorem is indeed valid.
3. The correct answer is $1-1/n$. The mistake occurs in the proof for $n=1$, when the formula on the left either may be assumed to be meaningless, or it may be assumed to be zero (since there are $n-1$ terms).
5. If n is prime, it is trivially a product of one or more primes. Otherwise n has factors, so $n=km$ for some k and m with $1\lt k$, $m\lt n$. Since both k and m are less than n, by induction they can be written as products of primes; hence n is the product of the primes appearing in the representations of k and m.
6. In the notation of Fig. 4, we prove A5 implies A6. This is clear since A5 implies $(a'-qa)m+(b'-qb)n=(a'm+b'n)-q(am+bn)=c-qd=r$.
7. $n^{2}-(n-1)^{2}+\cdots-(-1)^{n}1^{2}=1+2+\cdots+n=n(n+1)/2$.
8. (a) We must show that $(n^{2}-n+1)+(n^{2}-n+3)+\cdots+(n^{2}+n-1)$ equals $n^{3}$: And indeed, the sum is $n(n^{2}-n)+(1+3+\cdots+(2n-1))=n^{3}-n^{2}+n^{2}$, by Eq. (2). But an inductive proof was requested, so another approach should be taken! For $n=1$, the result is obvious. Let $n≥1$; we have $(n+1)^{2}-(n+1)=n^{2}-n+2n$, so the first terms for $n+1$ are $2n$ larger; thus the sum for $n+1$ is the sum for n plus
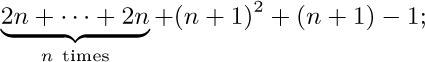
this equals $n^{3}+2n^{2}+n^{2}+3n+1=(n+1)^{3}$.
(b) We have shown that the first term for $(n+1)^{3}$ is two greater than the last term for $n^{3}$. Therefore by Eq. (2), $1^{3}+2^{3}+\cdots+n^{3}=$ sum of consecutive odd numbers starting with unity $=(\text{number of terms})^{2}=(1+2+\cdots+n)^{2}$.
10. Obvious for $n=10$. If $n≥10$, we have $2^{n+1}=2·2^{n}\gt (1+1/n)^{3}2^{n}$ and by induction this is greater than $(1+1/n)^{3}n^{3}=(n+1)^{3}$.
11. $(-1)^{n}(n+1)/(4(n+1)^{2}+1)$.
12. The only nontrivial part of the extension is the calculation of the integer q in E2. This can be done by repeated subtraction, reducing to the problem of determining whether $u+v\sqrt{2}$ is positive, negative, or zero, and the latter problem is readily solved.
It is easy to show that whenever $u+v\sqrt{2}=u'+v'\sqrt{2}$, we must have $u=u'$ and $v=v'$, since $\sqrt{2}$ is irrational. Now it is clear that 1 and $\sqrt{2}$ have no common divisor, if we define divisor in the sense that $u+v\sqrt{2}$ divides $a(u+v\sqrt{2})$ if and only if a is an integer. The algorithm extended in this way computes the regular continued fraction of the ratio of its inputs; see Section 4.5.3.
[Note: If we extend the concept of divisor so that $u+v\sqrt{2}$ divides $a(u+v\sqrt{2})$ if and only if a has the form $u'+v'\sqrt{2}$ for integers $u'$ and $v'$, there is a way to extend Algorithm E so that it always will terminate: If in step E2 we have $c=u+v\sqrt{2}$ and $d=u'+v'\sqrt{2}$, compute $c/d=c(u'-v'\sqrt{2})/(u'^{2}-2v'^{2})=x+y\sqrt{2}$ where x and y are rational. Now let $q=u''+v''\sqrt{2}$, where $u''$ and $v''$ are the nearest integers to x and y; and let $r=c-qd$. If $r=u'''+v'''\sqrt{2}$, it follows that $|u'''^{2}-2v'''^{2}|\lt|u'^{2}-2v'^{2}|$, hence the computation will terminate. See “quadratic Euclidean domains” in number theory texts.]
13. Add “$T≤3(n-d)+k$” to assertions A3, A4, A5, A6, where k takes the respective values 2, 3, 3, 1. Also add “$d\gt 0$” to A4.
15. (a) Let $A=S$ in (iii); every nonempty well-ordered set has a least element.
(b) Let $x≺y$ if $|x|\lt|y|$ or if $|x|=|y|$ and $x\lt 0 \lt y$.
(c) No, the subset of all positive reals fails to satisfy (iii). [Note: Using the so-called axiom of choice, a rather complicated argument can be given to show that every set can be well-ordered somehow; but nobody has yet been able to define an explicit relation that well-orders the real numbers.]
(d) To prove (iii) for $T_{n}$, use induction on n: Let A be a nonempty subset of $T_{n}$ and consider $A_{1}$, the set of first components of A. Since $A_{1}$ is a nonempty subset of S, and S is well-ordered, $A_{1}$ contains a smallest element x. Now consider $A_{x}$, the subset of A in which the first component equals x; $A_{x}$ may be considered a subset of $T_{n-1}$ if its first component is suppressed, so by induction $A_{x}$ contains a smallest element $(x,x_{2},\ldots,x_{n})$ that in fact is the smallest element of A.
(e) No, although properties (i) and (ii) are valid. If S contains at least two distinct elements, $a≺b$, the set $(b),(a,b),(a,a,b),(a,a,a,b),(a,a,a,a,b),\ldots$ has no least element. On the other hand T can be well-ordered if we define $(x_{1},\ldots,x_{m})≺(y_{1},\ldots,y_{n})$ whenever $m\lt n$, or $m=n$ and $(x_{1},\ldots,x_{n})≺(y_{1},\ldots,y_{n})$ in $T_{n}$.
(f) Let S be well-ordered by $≺$. If such an infinite sequence exists, the set A consisting of the members of the sequence fails to satisfy property (iii), for no element of the sequence can be smallest. Conversely if $≺$ is a relation satisfying (i) and (ii) but not (iii), let A be a nonempty subset of S that has no smallest element. Since A is not empty, we can find $x_{1}$ in A; since $x_{1}$ is not the smallest element of A, there is $x_{2}$ in A for which $x_{2}≺x_{1}$; since $x_{2}$ is not the smallest element either, we can find $x_{3}≺x_{2}$; etc.
(g) Let A be the set of all x for which $P(x)$ is false. If A is not empty, it contains a smallest element $x_{0}$. Hence $P(y)$ is true for all $y≺x_{0}$. But this implies $P(x_{0})$ is true, so $x_{0}$ is not in A (a contradiction). Therefore A must be empty: $P(x)$ is always true.
1. There is none; if r is a positive rational, $r/2$ is smaller.
2. Not if infinitely many nines appear in a row; in that case the decimal expansion of the number is $1+.24000000\ldots$, according to Eq. (2).
3. $-1/27$, but the text hasn’t defined it.
4. 4.
6. The decimal expansion of a number is unique, so $x=y$ if and only if $m=n$ and $d_{i}=e_{i}$ for all $i≥1$. If $x≠y$, one may compare m vs. n, $d_{1}$ vs. $e_{1}$, $d_{2}$ vs. $e_{2}$, etc.; when the first inequality occurs, the larger quantity belongs to the larger of $\{x,y\}$.
7. One may use induction on x, first proving the laws for x positive, and then for x negative. Details are omitted here.
8. By trying $n=0,1,2,\ldots$ we find the value of n for which $n^{m}≤u\lt(n+1)^{m}$. Assuming inductively that $n,d_{1},\ldots,d_{k-1}$ have been determined, $d_{k}$ is the digit such that
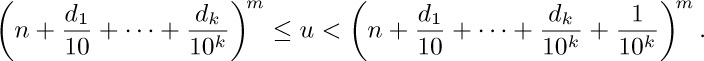
This construction can’t make $d_{k}=9$ for all $k\gt l$, because that could happen only if $(n+d_{1}/10+\cdots+d_{l}/10^{l}+1/10^{l})^{m}≤u$.
9. $((b^{p/q})^{u/v})^{qv}=(((b^{p/q})^{u/v})^{v})^{q}=((b^{p/q})^{u})^{q}=((b^{p/q})^{q})^{u}=b^{pu}$, hence $(b^{p/q})^{u/v}=b^{pu/qv}$. This proves the second law. We prove the first law using the second: $b^{p/q}b^{u/v}=(b^{1/qv})^{pv}(b^{1/qv})^{qu}=(b^{1/qv})^{pv+qu}=b^{p/q+u/v}$.
10. If $\log_{10}2=p/q$, with p and q positive, then $2^{q}=10^{p}$, which is absurd since the right-hand side is divisible by 5 but the left-hand side isn’t.
11. Infinitely many! No matter how many digits of x are given, we will not know whether $10^{x}=1.99999\ldots$ or $2.00000\ldots$, if x’s digits agree with the digits of $\log_{10}2$. There is nothing mysterious or paradoxical in this; a similar situation occurs in addition, if we are adding $.444444\ldots$ to $.55555\ldots$.
12. They are the only values of $d_{1},\ldots,d_{8}$ that satisfy Eq. (7).
13. (a) First prove by induction that if $y\gt 0$, $1+ny≤(1+y)^{n}$. Then set $y=x/n$, and take nth roots.
(b) $x=b-1$, $n=10^{k}$.
14. Set $x=\log_{b}c$ in the second equation of (5), then take logarithms of both sides.
15. Prove it, by transposing “$\log_{b}y$” to the other side of the equation and using (11).
17. 5; 1; 1; 0; undefined.
18. No, $\log_{8}x=\lg{x}/\lg{8}=\frac13\lg{x}$.
19. Yes, since $\lg n\lt(\log_{10}n)/.301\lt 14/.301\lt 47$.
20. They are reciprocals.
21. $(\ln\ln x-\ln\ln b)/\ln b$.
22. From the tables in Appendix A, $\lg x≈1.442695\ln x$; $\log_{10}x≈.4342945\ln x$. The relative error is $≈(1.442695-1.4342945)/1.442695≈0.582\%$.
23. Take the figure of area $\ln y$, and divide its height by x while multiplying its length by x. This deformation preserves its area and makes it congruent to the piece left when $\ln x$ is removed from $\ln xy$, since the height at point $x+xt$ in the diagram for $\ln xy$ is $1/(x+xt)=(1/(1+t))/x$.
24. Substitute 2 everywhere 10 appears.
25. Note that $z=2^{-p}\lfloor{2^{p-k}x}\rfloor\gt 0$, when p is the precision (the number of binary digits after the radix point). The quantity $y+\log_{b}x$ stays approximately constant.
27. Prove by induction on k that
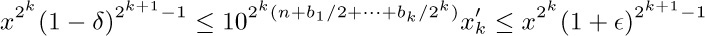
and take logarithms.
28. The following solution uses the same auxiliary table as before.
E1. [Initialize.] Set $x←1-\epsilon-x$, $y←y_{0}$, and $k←1$, where $1-\epsilon$ is the largest possible value of x, and $y_{0}$ is the nearest approximation to $b^{1-\epsilon}$. (The quantity $yb^{-x}$ will remain approximately constant in the following steps.)
E2. [Test for end.] If $x=0$, stop.
E3. [Compare.] If $x\lt\log_{b}(2^{k}/(2^{k}-1))$, increase k by 1 and repeat this step.
E4. [Reduce values.] Set $x←x-\log_{b}(2^{k}/(2^{k}-1))$, $y←y-(y\text{ shifted right }k)$, and go to E2. 
If y is set to $b^{1-\epsilon}(1+\epsilon_{0})$ in step E1, the subsequent computational error arises when $x←x+\log_{b}(1-2^{-k})+δ_{j}$ and $y←y(1-2^{-k})(1+\epsilon_{j})$ during the jth execution of step E4, for certain small errors $δ_{j}$ and $\epsilon_{j}$. When the algorithm terminates we have computed $y=b^{x-Σδ_{j}}∏_{j}(1+\epsilon_{j})$. Further analysis depends on b and the computer word size. Notice that both in this case and in exercise 26, it is possible to refine the error estimates somewhat if the base is e, since for most values of k the table entry $\ln(2^{k}/(2^{k}-1))$ can be given with high accuracy: It equals $2^{-k}+\frac{1}{2}2^{-2k}+\frac{1}{3}2^{-3k}+\cdots$.
Note: Similar algorithms can be given for trigonometric functions; see J. E. Meggitt, IBM J. Res. and Dev. 6 (1962), 210–226; 7 (1963), 237–245. See also T. C. Chen, IBM J. Res. and Dev. 16 (1972), 380–388; V. S. Linsky, Vychisl. Mat. 2 (1957), 90–119; D. E. Knuth, METAFONT: The Program (Reading, Mass.: Addison–Wesley, 1986), §120–§147.
29. e; 3; 4.
30. x.
1. $-a_{1}$; and $a_{2}+\cdots+a_{1}=0$. In general, sums with ‘$\cdots$’ are defined so that $(a_{p}+\cdots+a_{q})+(a_{q+1}+\cdots+a_{r})=a_{p}+\cdots+a_{r}$ for arbitrary integers p, q, and r.
2. $a_{1}+a_{2}+a_{3}$.
3. $\frac11+\frac13+\frac15+\frac17+\frac19+\frac{1}{11}$; $\frac19+\frac13+\frac11+\frac13+\frac19$. The rule for $p(j)$ is violated: In the first case $n^{2}=3$ occurs for no n, and in the second case $n^{2}=4$ occurs for two n. [See Eq. (18).]
4. $(a_{11})+(a_{21}+a_{22})+(a_{31}+a_{32}+a_{33})=(a_{11}+a_{21}+a_{31})+(a_{22}+a_{32})+(a_{33})$.
5. It is only necessary to use the rule $a∑_{R(i)}x_{i}=∑_{R(i)}(ax_{i})$:
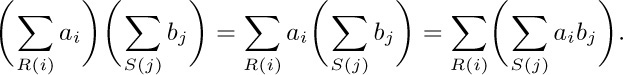
7. Use Eq. (3); the two limits are interchanged and the terms between $a_{0}$ and $a_{c}$ must be transferred from one limit to the other.
8. Let $a_{(i+1)i}=+1$, and $a_{i(i+1)}=-1$, for all i ≥ 0, and all other $a_{ij}$ zero; let $R(i)=S(i)=“i≥0”$. The left-hand side is −1, the right-hand side is +1.
9, 10. No; the applications of rule (d) assume that n ≥ 0. (The result is correct for n = −1 but the derivation isn’t.)
11. $(n+1)a$.
12. $\frac76(1-1/7^{n+1})$.
13. $m(n-m+1)+\frac12(n-m)(n-m+1)$; or, $\frac12(n(n+1)-m(m-1))$.
14. $\frac14(n(n+1)-m(m-1))(s(s+1)-r(r-1))$, if m ≤ n and r ≤ s.
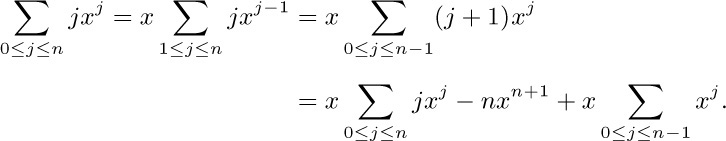
17. The number of elements in S.
18. $S'(j)=“1≤j\lt n”$. $R'(i,j)=$ “n is a multiple of i and $i\gt j$”.
19. $(a_{n}-a_{m-1}) [m≤n]$.
20. $(b-1)\sum_{k=0}^{n}(n-k)b^{k}+n+1=\sum_{k=0}^{n}b^{k}$; this formula follows from (14) and the result of exercise 16.
21. $∑_{R(j)}a_{j}+∑_{S(j)}a_{j}=∑_{j}a_{j}[R(j)]+∑_{j}a_{j}[S(j)]=∑_{j}a_{j}([R(j)]+[S(j)])$; now use the fact that $[R(j)]+[S(j)]=[R(j)\text{ or }S(j)]+[R(j)\text{ and }S(j)]$. In general, bracket notation gives us the ability to manipulate “on the line” instead of “below the line.”
22. For (5) and (7), just change ∑ to ∏. We also have $∏_{R(i)}b_{i}c_{i}=(∏_{R(i)}b_{i})(∏_{R(i)}c_{i})$ and
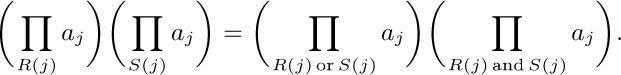
23. 0 + x = x and $1·x=x$. This makes many operations and equations simpler, such as rule (d) and its analog in the previous exercise.
25. The first step and last step are OK. The second step uses i for two different purposes at once. The third step should probably be $∑_{i=1}^{n}n$.
26. Key steps, after transforming the problem as in Example 2:
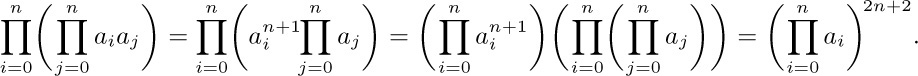
The answer is $\left(∏_{i=0}^{n}a_{i}\right)^{n+2}$.
28. $(n+1)/2n$.
29. (a) $∑_{0≤k≤j≤i≤n}a_{i}a_{j}a_{k}$. (b) Let $S_r=∑_{i=0}^{n}a_{i}^{r}$. Solutions: $\frac{1}{3}S_3+\frac{1}{2}S_1S_2+\frac{1}{6}S_{1}^{3}$. The general solution to this problem, as the number of indices gets larger, may be found in Section 1.2.9, Eq. (38).
30. Write the left side as $∑_{1≤j,k≤n}a_{j}b_{k}x_{j}y_{k}$, and do a similar thing on the right. (This identity is the special case m = 2 of exercise 46.)
31. Set $a_{j}=u_{j}$, $b_{j}=1$, $x_{j}=v_{j}$, and $y_{j}=1$, to obtain the answer $n∑_{j=1}^{n}u_{j}v_{j}-(∑_{j=1}^{n}u_j)(∑_{j=1}^{n}v_j)$. Consequently we have $(∑_{j=1}^{n}u_{j})(∑_{j=1}^{n}v_{j})≤n∑_{j=1}^{n}u_{j}v_{j}$ when $u_{1}≤u_{2}≤\cdots≤u_{n}$ and $v_{1}≤v_{2}≤\cdots≤v_{n}$, a result known as Chebyshev’s monotonic inequality. [See Soobshch. mat. obshch. Khar, kovskom Univ. 4, 2 (1882), 93–98.]
33. This can be proved by induction on n, if we rewrite the formula as
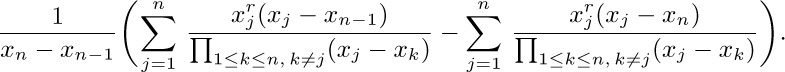
Each of these sums now has the form of the original sum, except on $n-1$ elements, and the values turn out nicely by induction when $0≤r≤n-1$. When r = n, consider the identity
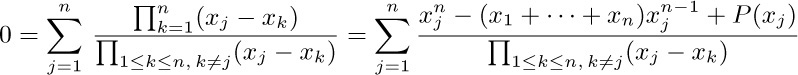
where $P(x_{j})$ is a polynomial of degree $n-2$ in $x_{j}$ whose coefficients are symmetric functions of $\{x_{1},\ldots,x_{n}\}$ that don’t depend on j. (See exercise 1.2.9–10.) We obtain the desired answer from the solutions for $r=0,1,\ldots,n-1$.
Notes: Dr. Matrix was anticipated in this discovery by L. Euler, who wrote to Christian Goldbach about it on 9 November 1762. See Euler’s Institutionum Calculi Integralis 2 (1769),§1169; and E. Waring, Phil. Trans. 69 (1779), 64–67. The following alternative method of proof, using complex variable theory, is less elementary but more elegant: By the residue theorem, the value of the given sum is
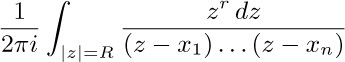
where $R\gt|x_{1}|,\ldots,|x_{n}|$. The Laurent expansion of the integrand converges uniformly on $|z|=R$; it is
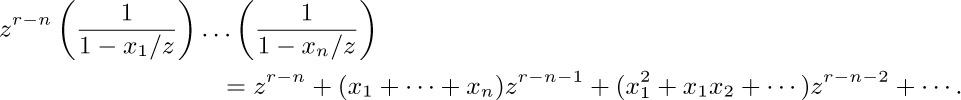
Integrating term by term, everything vanishes except the coefficient of $z^{-1}$. This method gives us the general formula for an arbitrary integer $r≥0$:
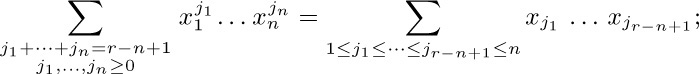
see Eq. 1.2.9–(33). [J. J. Sylvester, Quart. J. Math. 1 (1857), 141–152.]
34. If the reader has tried earnestly to solve this problem, without getting the answer, perhaps its purpose has been achieved. The temptation to regard the numerators as polynomials in x rather than as polynomials in k is almost overwhelming. It would undoubtedly be easier to prove the considerably more general result
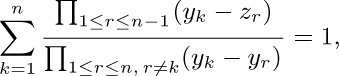
which is an identity in $2n-1$ variables!
35. If $R(j)$ never holds, the value should be $-∞$. The stated analog of rule (a) is based on the identity $a+\max(b,c)=\max(a+b,a+c)$. Similarly if all $a_{i}$, $b_{j}$ are nonnegative, we have
$\sup_{R(i)}a_{i}\sup_{S(j)}b_{j}=\sup_{R(i)}\sup_{S(j)}a_{i}b_{j}$.
Rules (b), (c) do not change; for rule (d) we get the simpler form
$\sup(\sup_{R(j)}a_{j},\sup_{S(j)}a_{j})=\sup_{R(j)\text{ or }S(j)}a_{j}$.
36. Subtract column one from columns $2,\ldots,n$. Add rows $2,\ldots,n$ to row one. The result is a triangular determinant.
37. Subtract column one from columns $2,\ldots,n$. Then subtract $x_{1}$ times row k − 1 from row k, for $k=n,n-1,\ldots,2$ (in that order). Now factor $x_{1}$ out of the first column and factor $x_{k}-x_{1}$ out of columns $k=2,\ldots,n$, obtaining $x_{1}(x_{2}-x_{1})\ldots(x_{n}-x_{1})$ times a Vandermonde determinant of order n − 1. The process continues by induction.
Alternative proof, using “higher” mathematics: The determinant is a polynomial in the variables $x_{1},\ldots,x_{n}$ of total degree $1+2+\cdots+n$. It vanishes if $x_{j}=0$ or if $x_{i}=x_{j}$ $(i\lt j)$, and the coefficient of $x_{1}^{1}x_{2}^{2}\ldots x_{n}^{n}$ is +1. These facts characterize its value. In general, if two rows of a matrix become equal for $x_{i}=x_{j}$, their difference is usually divisible by $x_{i}-x_{j}$, and this observation often speeds the evaluation of determinants.
38. Subtract column one from columns $2,\ldots,n$, and factor out
$(x_{1}+y_{1})^{-1}\ldots(x_{n}+y_{1})^{-1}(y_{1}-y_{2})\ldots(y_{1}-y_{n})$
from rows and columns. Now subtract row one from rows $2,\ldots,n$ and factor out $(x_{1}-x_{2})\ldots(x_{1}-x_{n})(x_{1}+y_{2})^{-1}\ldots(x_{1}+y_{n})^{-1}$; we are left with the Cauchy determinant of order n − 1.
39. Let I be the identity matrix $(δ_{ij})$, and J the matrix of all ones. Since $J^{2}=nJ$, we have $(xI+yJ)((x+ny)I-yJ)=x(x+ny)I$.
40. [A. de Moivre, The Doctrine of Chances, 2nd edition (London: 1738), 197–199.] We have
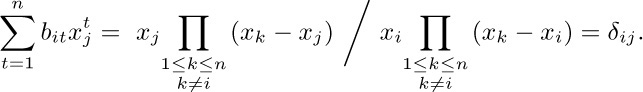
41. This follows immediately from the relation of an inverse matrix to its cofactors. It may also be interesting to give a direct proof here: We have
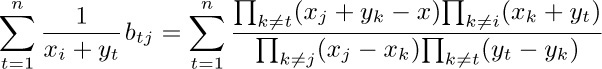
when $x=0$. This is a polynomial of degree at most $n-1$ in x. If we set $x=x_{j}+y_{s}$, $1≤s≤n$, the terms are zero except when $s=t$, so the value of this polynomial is
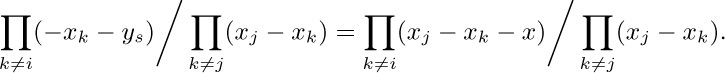
These polynomials of degree at most $n-1$ agree at n distinct points x, so they agree also for $x=0$; hence
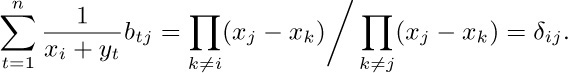
42. $n/(x+ny)$.
43. $1-∏_{k=1}^{n}(1-1/x_{k})$. This is easily verified if any $x_{i}=1$, since the inverse of any matrix having a row or column all of ones must have elements whose sum is 1. If none of the $x_{i}$ equals one, sum the elements of row i by setting x = 1 in exercise 40 and obtaining $∏_{k≠i}(x_{k}-1)/x_{i}∏_{k≠i}(x_{k}-x_{i})$. After multiplying numerator and denominator by $x_{i}-1$, we can sum on i by applying exercise 33 with r = 0 to the n + 2 numbers $\{0,1,x_{1},\ldots,x_{n}\}$.
44. We find
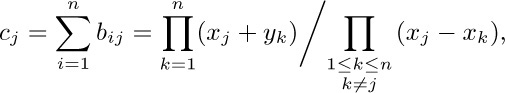
after applying exercise 33. And
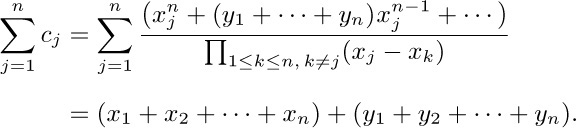
45. Let $x_{i}=i$, $y_{j}=j-1$. From exercise 44, the sum of the elements of the inverse is $(1+2+\cdots+n)+((n-1)+(n-2)+\cdots+0)=n^{2}$. From exercise 38, the elements of the inverse are
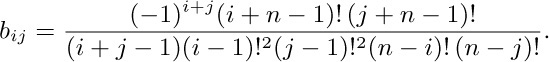
This quantity can be put into several forms involving binomial coefficients, for example
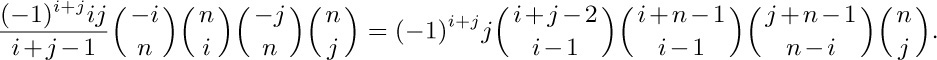
From the latter formula we see that $b_{ij}$ is not only an integer, it is divisible by $i$, $j$, $n$, $i+j-1$, $i+n-1$, $j+n-1$, $n-i+1$, and $n-j+1$. Perhaps the prettiest formula for $b_{ij}$ is
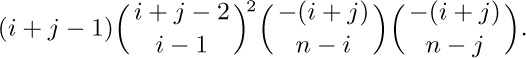
The solution to this problem would be extremely difficult if we had not realized that a Hilbert matrix is a special case of a Cauchy matrix; the more general problem is much easier to solve than its special case! It is frequently wise to generalize a problem to its “inductive closure,” i.e., to the smallest generalization such that all subproblems that arise in an attempted proof by mathematical induction belong to the same class. In this case, we see that cofactors of a Cauchy matrix are determinants of Cauchy matrices, but cofactors of Hilbert matrices are not determinants of Hilbert matrices. [For further information, see J. Todd, J. Research Nat. Bur. Stand. 65 (1961), 19–22; A. Cauchy, Exercices d’analyse et de physique mathématique 2 (1841), 151–159.]
46. For any integers $k_{1},k_{2},\ldots,k_{m}$, let $\epsilon(k_{1},\ldots,k_{m})={\rm sign}{(∏_{1≤i\lt j≤m}(k_{j}-k_{i}))}$, where sign $x=[x\gt 0]-[x\lt 0]$. If $(l_{1},\ldots,l_{m})$ is equal to $(k_{1},\ldots,k_{m})$ except for the fact that $k_{i}$ and $k_{j}$ have been interchanged, we have $\epsilon(l_{1},\ldots,l_{m})=-\epsilon(k_{1},\ldots,k_{m})$. Therefore we have the equation $\det(B_{k_{1}\ldots k_{m}})=\epsilon(k_{1},\ldots,k_{m})\det(B_{j_{1}\ldots j_{m}})$, if $j_{1}≤\cdots≤j_{m}$ are the numbers $k_{1},\ldots,k_{m}$ rearranged into nondecreasing order. Now by definition of the determinant,
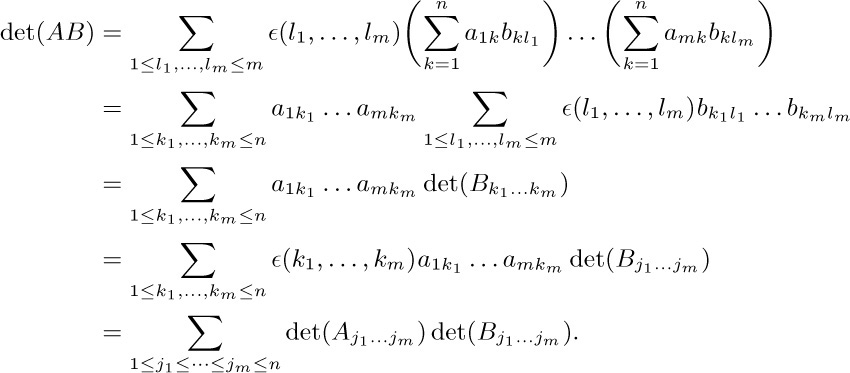
Finally, if $j_{i}=j_{i+1}$, $\det(A_{j_{1}\ldots j_{m}})=0$. [J. de l’École Polytechnique 9 (1813), 280–354; 10 (1815), 29–112. Binet and Cauchy presented their papers on the same day in 1812.]
47. Let $a_{ij}=(∏_{k=1}^{j-1}(x_{i}+p_{k}))(∏_{k=j+1}^{n}(x_{i}+q_{k}))$. Subtract column k − 1 from column k and factor out $p_{k-j}-q_{k}$, for $k=n,n-1,\ldots,j+1$ (in that order), for $j=1,2,\ldots,n-1$ (in that order). This leaves $∏_{1≤i\lt j≤n}(p_{i}-q_{j})$ times $\det(b_{ij})$ where $b_{ij}=∏_{k=j+1}^{n}(x_{i}+q_{k})$. Now subtract $q_{k+j}$ times column k + 1 from column k for $k=1,\ldots,n-j$, and for $j=1,\ldots,n-1$; this leaves $\det(c_{ij})$, where $c_{ij}=x_{i}^{n-j}$ essentially defines a Vandermonde matrix. We can now proceed as in exercise 37, operating on rows instead of columns, obtaining
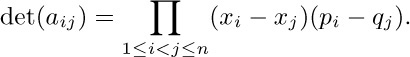
When $p_{j}=q_{j}=y_{j}$ for $1≤j≤n$, the matrix in this exercise is a Cauchy matrix with row i multiplied by $∏_{j=1}^{n}(x_{i}+y_{j})$. Therefore this result generalizes exercise 38 by adding $n-2$ independent parameters. [Manuscripta Math. 69 (1990), 177–178.]
1. 1,−2, −1, 0, 5.
2. $\lfloor{x}\rfloor$.
3. By definition, $\lfloor{x}\rfloor$ is the greatest integer less than or equal to x; therefore $\lfloor{x}\rfloor$ is an integer, $\lfloor{x}\rfloor≤x$, and $\lfloor{x}\rfloor+1\gt x$. The latter properties, plus the fact that when m and n are integers we have $m\lt n$ if and only if $m≤n-1$, lead to an easy proof of propositions (a) and (b). Similar arguments prove (c) and (d). Finally, (e) and (f) are just combinations of previous parts of this exercise.
4. By part (f), $x\le\lceil{x}\rceil\lt x+1$; hence $-x-1\lt\lceil{x}\rceil\le-x$; use part (e).
5. $\lfloor{x+\frac12}\rfloor$. The value of $(-x\text{ rounded})$ will be the same as $-(x\text{ rounded})$, except when $x\bmod1=\frac12$. In the latter case, the negative value is rounded towards zero and the positive value is rounded away from zero.
6. (a) is true: $\lfloor{\sqrt{x}}\rfloor=n⇔n^{2}≤x\lt(n+1)^{2}⇔$ $n^{2}≤\lfloor{x}\rfloor\lt(n+1)^{2}⇔$ $\lfloor{\sqrt{\lfloor{x}\rfloor}}\rfloor=n$. Similarly, (b) is true. But (c) fails when x is, say, 1.1.
7. $\lfloor{x+y}\rfloor=\lfloor{\lfloor{x}\rfloor+x\bmod 1+\lfloor{y}\rfloor+y\bmod 1}\rfloor=$ $\lfloor{x}\rfloor+\lfloor{y}\rfloor+\lfloor{x\bmod 1+y\bmod 1}\rfloor$. The inequality should be ≥ for ceilings, and then equality holds if and only if either x or y is an integer or $x\bmod 1+y\bmod 1\gt 1$; that is, if and only if $(-x)\bmod1+(-y)\bmod1\lt 1$.
8. 1, 2, 5, −100.
9. −1, 0, −2.
10. 0.1, 0.01, −0.09.
11. x = y.
12. All.
13. +1, −1.
14. 8.
15. Multiply both sides of Eq. (1) by z; the result is also easily verified if $y=0$.
17. As an example, consider the multiplication portion of Law A: We have $a=b+qm$ and $x=y+rm$, for some integers q and r; so $ax=by+(br+yq+qrm)m$.
18. We have $a-b=kr$ for some integer k, and also $kr≡\md[0]{s}$. Hence by Law B, $k≡\md[0]{s}$, so $a-b=qsr$ for some integer q.
20. Multiply both sides of the congruence by a′.
21. There is at least one such representation, by the previously proved exercise. If there are two representations, $n=p_{1}\ldots p_{k}=q_{1}\ldots q_{m}$, we have $q_{1}\ldots q_{m}≡\md[0]{p_{1}}$; so if none of the q’s equals $p_{1}$ we could cancel them all by Law B and obtain $1≡\md[0]{p_{1}}$. The latter is impossible since $p_{1}$ is not equal to 1. So some $q_{j}$ equals $p_{1}$, and $n/p_{1}=p_{2}\ldots p_{k}=q_{1}\ldots q_{j-1}q_{j+1}\ldots q_{m}$. Either n is prime, when the result is clearly true, or by induction the two factorizations of $n/p_{1}$ are the same.
22. Let $m=ax$, where $a\gt 1$ and $x\gt 0$. Then $ax≡0$ but $x\not\equiv\md[0]{m}$.
24. Law A is always valid for addition and subtraction; Law C is always valid.
26. If b is not a multiple of p, then $b^{2}-1$ is, so one of the factors must be.
27. A number is relatively prime to $p^{e}$ if and only if it is not a multiple of p. So we count those that are not multiples of p and get $\varphi(p^{e})=p^{e}-p^{e-1}$.
28. If a and b are relatively prime to m, so is ab mod m, since any prime dividing the latter and m must divide a or b also. Now simply let $x_{1},\ldots,x_{\varphi(m)}$ be the numbers relatively prime to m, and observe that $ax_{1}\bmod m,\ldots,ax_{\varphi(m)}\bmod m$ are the same numbers in some order, etc.
29. We prove (b): If $r⊥ s$ and if $k^{2}$ divides rs, then $p^{2}$ divides rs for some prime p, so p divides r (say) and cannot divide s; so $p^{2}$ divides r. We see that $f(rs)=0$ if and only if $f(r)=0$ or $f(s)=0$.
30. Suppose $r⊥s$. One idea is to prove that the $\varphi(rs)$ numbers relatively prime to rs are precisely the $\varphi(r)\varphi(s)$ distinct numbers $(sx_{i}+ry_{j})\bmod(rs)$ where $x_{1},\ldots,x_{\varphi(r)}$ and $y_{1},\ldots,y_{\varphi(s)}$ are the corresponding values for r and s.
Since $\varphi$ is multiplicative, $\varphi(10^{6})=\varphi(2^{6})\varphi(5^{6})=(2^{6}-2^{5})(5^{6}-5^{5})=400000$. And in general when $n=p_{1}^{\large e_{1}}\ldots p_{r}^{\large e_{r}}$, we have $\varphi(n)=(p_{1}^{\large e_{1}}-p_{1}^{{\large e_{1}}-1})\ldots(p_{r}^{\large e_{r}}-p_{r}^{{\large e_{r}}-1})=n∏_{p\backslash n,\,p\text{ prime}}(1-1/p)$. (Another proof appears in exercise 1.3.3–27.)
31. Use the fact that the divisors of rs may be uniquely written in the form cd where c divides r and d divides s. Similarly, if $f(n)≥0$, one can show that the function $\max_{d\backslash n}f(d)$ is multiplicative (see exercise 1.2.3–35).
33. Either $n+m$ or $n-m+1$ is even, so one of the quantities inside the brackets is an integer; so equality holds in exercise 7, and we obtain (a) n; (b) n + 1.
34. b must be an integer ≥ 2. (Set $x=b$.) The sufficiency is proved as in exercise 6. The same condition is necessary and sufficient for $\lceil{\log_{b}x}\rceil=\lceil{\log_{b}\lceil{x}\rceil}\rceil$.
Note: R. J. McEliece has pointed out the following generalization: Let $f$ be a continuous, strictly increasing function defined on an interval A, and assume that both $\lfloor{x}\rfloor$ and $\lceil{x}\rceil$ are in A whenever x is in A. Then the relation $\lfloor{f(x)}\rfloor=\lfloor{f(\lfloor{x}\rfloor)}\rfloor$ holds for all x in A if and only if the relation $\lceil{f(x)}\rceil=\lceil{f(\lceil{x}\rceil)}\rceil$ holds for all x in A, if and only if the following condition is satisfied for all x in A: “$f(x)$ is an integer implies x is an integer.” The condition is obviously necessary, for if $f(x)$ is an integer and it equals $\lfloor{f(\lfloor{x}\rfloor)}\rfloor$ or $\lceil{f(\lceil{x}\rceil)}\rceil$ then x must equal $\lfloor{x}\rfloor$ or $\lceil{x}\rceil$. Conversely if, say, $\lfloor{f(\lfloor{x}\rfloor)}\rfloor\lt\lfloor{f(x)}\rfloor$ then by continuity there is some y with $\lfloor{x}\rfloor\lt y≤x$ for which $f(y)$ is an integer; but y cannot be an integer.
35. $\large\frac{x+m}{n}-1=\frac{x+m}{n}-\frac{1}{n}-\frac{n-1}{n}\lt$ $\frac{\lfloor{x}\rfloor+m}{n}-\frac{n-1}{n}≤\left\lfloor{\frac{\lfloor{x}\rfloor+m}{n}}\right\rfloor≤\frac{x+m}{n}$; apply exercise 3. Use of exercise 4 gives a similar result for the ceiling function. Both identities follow as a special case of McEliece’s theorem in exercise 34.
36. Assume first that $n=2t$. Then
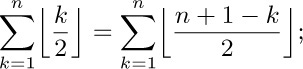
hence
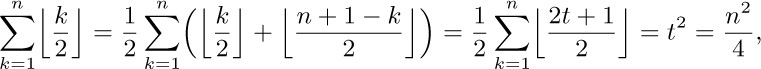
by exercise 33. And if $n=2t+1$, we have $t^{2}+\lfloor{n/2}\rfloor=t^{2}+t=n^{2}/4-1/4$. For the second sum we get, similarly, $\lceil{n(n+2)/4}\rceil$.
37. $\displaystyle\sum_{0≤k\lt n}\frac{mk+x}{n}=\frac{m(n-1)}{2}+x$. Let $\{y\}$ denote $y\bmod1$; we must subtract
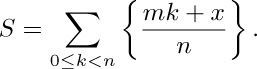
This quantity S consists of d copies of the same sum, since if $t=n/d$ we have
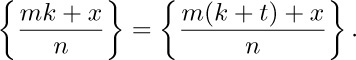
Let $u=m/d$; then
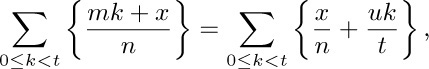
and since $t⊥u$ this sum may be rearranged to equal
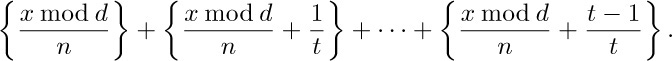
Finally, since $(x\bmod d)/n\lt 1/t$, the braces in this sum may be removed and we have
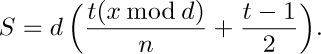
An application of exercise 4 yields the similar identity
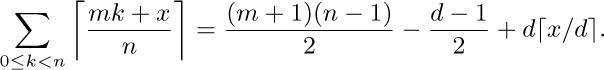
This formula would become symmetric in m and n if it were extended over the range $0\lt k≤n$. (The symmetry can be explained by drawing the graph of the summand as a function of k, then reflecting about the line $y=x$.)
38. Both sides increase by $\lceil{y}\rceil$ when x increases by 1, so we can assume that $0≤x\lt 1$. Then both sides are zero when $x=0$, and both sides increase by 1 when x increases past the values $1-k/y$ for $y\gt k≥0$. [Crelle 136 (1909), 42; the case $y=n$ is due to C. Hermite, Acta Math. 5 (1884), 315.]
39. Proof of part (f): Consider the more general identity $∏_{0≤k\lt n}2\sin π(x+k/n)=2\sin πnx$, which can be demonstrated as follows: Since $2\sinθ=(e^{iθ}-e^{-iθ})/i=(1-e^{-2iθ})e^{iθ-iπ/2}$, the identity is a consequence of the two formulas
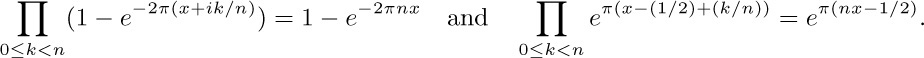
The latter is true since the function $x-\frac12$ is replicative; and the former is true because we may set $z=1$ in the factorization of the polynomial $z^{n}-α^{n}=(z-α)(z-ωα)\ldots(z-ω^{n-1}α)$, where $ω=e^{-2πi/n}$.
40. (Note by N. G. de Bruijn.) If $f$ is replicative, $f(nx+1)-f(nx)=f(x+1)-f(x)$ for all $n\gt 0$. Hence if $f$ is continuous, $f(x+1)-f(x)=c$ for all x, and $g(x)=f(x)-c\lfloor{x}\rfloor$ is replicative and periodic. Now
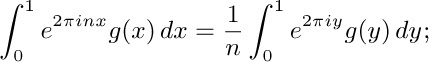
expanding in Fourier series shows that $g(x)=(x-\frac12)a$ for $0\lt x\lt 1$. It follows that $f(x)=(x-\frac12)a$. In general, this argument shows that any replicative locally Riemann-integrable function has the form $(x-\frac12)a+b\max(\lfloor{x}\rfloor,0)+c\min(\lfloor{x}\rfloor,0)$ almost everywhere. For further results see L. J. Mordell, J. London Math. Soc. 33 (1958), 371–375; M. F. Yoder, Æquationes Mathematicæ 13 (1975), 251–261.
41. We want $a_{n}=k$ when $\frac{1}{2}k(k-1)\lt n≤\frac{1}{2}k(k+1)$. Since n is an integer, this is equivalent to
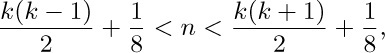
i.e., $k-\frac12\lt\sqrt{2n}\lt k+\frac12$. Hence $a_n=\lfloor{\sqrt{2n}+\frac12}\rfloor$, the nearest integer to $\sqrt{2n}$. Other correct answers are $\lceil{\sqrt{2n}-\frac12}\rceil$, $\lceil{(\sqrt{8n+1}-1)/2}\rceil$, $\lfloor{(\sqrt{8n-7}+1)/2}\rfloor$, etc.
42. (a) See exercise 1.2.7–10. (b) The given sum is $n\lfloor{\log_{b}n}\rfloor-S$, where
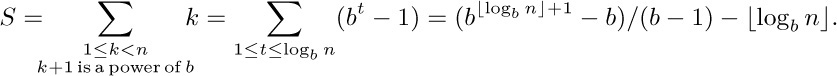
43. $\lfloor{\sqrt{n}}\rfloor(n-\frac{1}{6}(2\lfloor{\sqrt{n}}\rfloor+5)(\lfloor{\sqrt{n}}\rfloor-1))$.
44. The sum is $n+1$ when n is negative.
45. $\lfloor{mj/n}\rfloor=r$ if and only if $\displaystyle\left\lceil\frac{rn}{m}\right\rceil≤j\lt{\left\lceil{\smash{\frac{(r+1)n}{m}}\vphantom{\frac12}}\right\rceil}$, and we find that the given sum is therefore
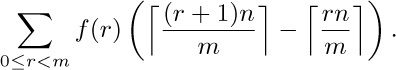
The stated result follows by rearranging the latter sum, grouping the terms with a particular value of $\lceil{rn/m}\rceil$. The second formula is immediate by the substitution
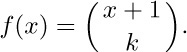
46. $∑_{0≤j\lt αn}f(\lfloor{mj/n}\rfloor)=$ $∑_{0≤r\lt αm}\lceil{rn/m}\rceil(f(r-1)-f(r))+\lceil{αn}\rceil f(\lceil{αm}\rceil-1)$.
47. (a) The numbers $2,4,\ldots,p-1$ are the even residues (modulo p); since $2kq=p\lfloor{2kq/p}\rfloor+(2kq)\bmod p$, the number $(-1)^{\lfloor{2kq/p}\rfloor}((2kq)\bmod p)$ will be an even residue or an even residue minus p, and each even residue clearly occurs just once. Hence $(-1)^{σ}q^{(p-1)/2}2·4\ldots(p-1)≡2·4\ldots(p-1)$.
(b) Let $q=2$. If $p=4n+1$, $σ=n$; if $p=4n+3,σ=n+1$. Hence $\left(\frac{2}{p}\right)=(1,-1,-1,1)$ according as $p\bmod 8=(1,3,5,7)$, respectively.
(c) For $k\lt p/4$, we have
$\lfloor{(p-1-2k)q/p}\rfloor=q-\lceil{(2k+1)q/p}\rceil=q-1-\lfloor{(2k+1)q/p}\rfloor≡\md[\lfloor{(2k+1)q/p}\rfloor]{2}$.
Hence we may replace the last terms $\lfloor{(p-1)q/p}\rfloor,\lfloor{(p-3)q/p}\rfloor,\ldots$ by $\lfloor{q/p}\rfloor,\lfloor{3q/p}\rfloor$, etc. (d) $∑_{0≤k\lt p/2}\lfloor{kq/p}\rfloor+∑_{0≤r\lt q/2}\lceil{rp/q}\rceil=\lceil{p/2}\rceil(\lceil{q/2}\rceil-1)=(p+1)(q-1)/4$. Also $∑_{0≤r\lt q/2}\lceil{rp/q}\rceil=∑_{0≤r\lt q/2}\lfloor{rp/q}\rfloor+(q-1)/2$. The idea of this proof goes back to G. Eisenstein, Crelle 28 (1844), 246–248; Eisenstein also gave several other proofs of this and other reciprocity laws in the same volume.
48. (a) This is clearly not always true when $n\lt 0$; when $n\gt 0$ it is easy to verify.
(b) $\lfloor{(n+2-\lfloor{n/25}\rfloor)/3}\rfloor=\lceil{(n-\lfloor{n/25}\rfloor)/3}\rceil=$ $\lceil{(n+\lceil{-n/25}\rceil)/3}\rceil=\lceil{\lceil{24n/25}\rceil/3}\rceil=$ $\lceil{8n/25}\rceil=\lfloor{(8n+24)/25}\rfloor$. The penultimate equality is justified by exercise 35.
49. Since $f(0)=f(f(0))=f(f(0)+0)=f(0)+f(0)$, we have $f(n)=n$ for all integers n. If ${\large f}{\left(\frac12\right)}=k≤0$, we have $k={\large f}{\left(\frac{1}{1-2k}{\large f}{\left(\frac{1}{2}-k\right)}\right)}={\large f}{\left(\frac{1}{1-2k}\left({\large f}{\left(\frac{1}{2}\right)}-k\right)\right)}=f(0)=0$. And if ${\large f}{\left(\frac{1}{n-1}\right)}=0$ we have ${\large f}{\left(\frac{1}{n}\right)}={\large f}{\left(\frac{1}{n}{\large f}{\left(1+\frac{1}{n-1}\right)}\right)}={\large f}{\left(\frac{1}{n-1}\right)}=0$; furthermore $1≤m\lt n$ implies ${\large f}{\left(\frac{m}{n}\right)}={\large f}{\left(\frac{1}{a}{\large f}{\left(\frac{am}{n}\right)}\right)}={\large f}{\left(\frac{1}{a}\right)}=0$, for $a=\lceil{n/m}\rceil$, by induction on m. Thus ${\large f}{\left(\frac12\right)}≤0$ implies $f(x)=\lfloor{x}\rfloor$ for all rational x. On the other hand, if ${\large f}{\left(\frac12\right)}\gt0$ the function $g(x)=-f(-x)$ satisfies (i) and (ii) and has ${\large g}{\left(\frac12\right)}=1-{\large f}{\left(\frac12\right)}≤0$; hence $f(x)=-g(-x)=-\lfloor{-x}\rfloor=\lceil{x}\rceil$ for all rational x. [P. Eisele and K. P. Hadeler, AMM 97 (1990), 475–477.]
It does not follow, however, that $f(x)=\lfloor{x}\rfloor$ or $\lceil{x}\rceil$ for all real values of x. If, for example, $h(x)$ is any function with $h(1)=1$ and $h(x+y)=h(x)+h(y)$ for all real x and y, then the function $f(x)=\lfloor{h(x)}\rfloor$ satisfies (i) and (ii); but $h(x)$ may be unbounded and highly erratic when $0\lt x\lt 1$ [G. Hamel, Math. Annalen 60 (1905), 459–462].
1. 52!. For the curious, this number is 806 58175 17094 38785 71660 63685 64037 66975 28950 54408 83277 82400 00000 00000. (!)
2. $p_{nk}=p_{n(k-1)}(n-k+1)$. After the first $n-1$ objects have been placed, there is only one possibility for the last object.
3. 5 3 1 2 4, 3 5 1 2 4, 3 1 5 2 4, 3 1 2 5 4, 3 1 2 4 5; 4 2 3 5 1, 4 1 3 5 2, 4 1 2 5 3, 3 1 2 5 4, 3 1 2 4 5.
4. There are 2568 digits. The leading digit is 4 (since $\log_{10}4=2\log_{10}2 ≈ .602$). The least significant digit is zero, and in fact by Eq. (8) the low order 249 digits are all zero. The exact value of 1000! was calculated by H. S. Uhler using a desk calculator and much patience over a period of several years, and appears in Scripta Mathematica 21 (1955), 266–267. It begins with 402 38726 00770 … . (The last step in the calculation, to multiply the two numbers 750! and $\prod_{k=751}^{1000}k$, was performed on UNIVAC I by John W. Wrench, Jr., “in the extraordinary time of 2½ minutes.” Nowadays, of course, a desktop machine easily produces 1000! in a fraction of a second, and we can confirm that Uhler’s value was 100% correct.)
5. $(39902)(97/96)≈416+39902=40318$.
6. $2^{18}·3^{8}·5^{4}·7^{2}·11·13·17·19$.
8. It is $\lim_{m→∞}m^{n}m!/((n+m)!/n!)=n!\lim_{m→∞}m^{n}/((m+1)\ldots(m+n))=n!$, since $m/(m+k)→1$.
9. $\sqrt{\pi}$ and $-2\sqrt{\pi}$. (Exercise 10 used.)
10. Yes, except when x is zero or a negative integer. For we have
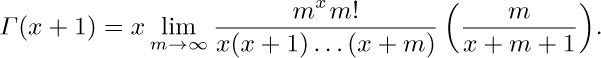
13. For each n, $1≤n\lt p$, determine $n'$ as in exercise 1.2.4–19. There is exactly one such $n'$, by Law 1.2.4B; and $(n')'=n$. Therefore we can pair off the numbers in groups of two, provided that $n'≠n$. If $n'=n$, we have $n^{2}≡\md[1]{p}$; hence, as in exercise 1.2.4–26, $n=1$ or $n=p-1$. So $(p-1)!≡ 1·1\ldots1·(-1)$, since 1 and $p-1$ are the only unpaired elements.
14. Among the numbers $\{1,2,\ldots,n\}$ that are not multiples of p, there are $\lfloor{n/p}\rfloor$ complete sets of $p-1$ consecutive elements, each with a product congruent to $\md[-1]{p}$ by Wilson’s theorem. There are also $a_{0}$ left over, which are congruent to $\md[a_{0}!]{p}$; so the contribution from the factors that are not multiples of p is $(-1)^{\lfloor{n/p}\rfloor}a_{0}!$. The contribution from the factors that are multiples of p is the same as the contribution in $\lfloor{n/p}\rfloor !$; this argument can therefore be repeated to get the desired formula.
15. $(n!)^{3}$. There are $n!$ terms. Each term has one entry from each row and each column, so it has the value $(n!)^{2}$.
16. The terms do not approach zero, since the coefficients approach $1/e$.
17. Express the gamma functions as limits by Eq. (15).
18. $\displaystyle\prod_{n≥1}\frac{n}{n-\frac12}\frac{n}{n+\frac12}=\frac{\varGamma(\frac12)\varGamma(\frac32)}{\varGamma(1)\varGamma(1)}=2\varGamma(\frac32)^{2}$.
[Wallis’s own heuristic “proof” can be found in D. J. Struik’s Source Book in Mathematics (Harvard University Press, 1969), 244–253.]
19. Change of variable $t=mt$, integration by parts, and induction.
20. [For completeness, we prove the stated inequality. Start with the easily verified inequality $1+x≤e^{x}$; set $x=±t/n$ and raise to the nth power to get $(1±t/n)^{n}≤e^{±t}$. Hence $e^{-t}≥(1-t/n)^{n}=e^{-t}(1-t/n)^{n}e^{t}≥$ $e^{-t}(1-t/n)^{n}(1+t/n)^{n}=$ $e^{-t}(1-t^{2}/n^{2})^{n}≥e^{-t}(1-t^{2}/n)$ by exercise 1.2.1–9.]
Now the given integral minus $\varGamma_{m}(x)$ is
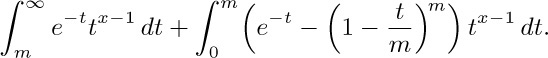
As $m→∞$, the first of these integrals approaches zero, since $t^{x-1}\lt e^{t/2}$ for large t; and the second is less than
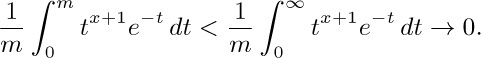
21. If $c(n,j,k_{1},k_{2},\ldots)$ denotes the appropriate coefficient, we find
$c(n+1,j,k_{1},\ldots)=c(n,j-1,k_{1}-1,k_{2},\ldots)+$ $(k_{1}+1)c(n,j,k_{1}+1,k_{2}-1,k_{3},\ldots)+$ $(k_{2}+1)c(n,j,k_{1},k_{2}+1,k_{3}-1,k_{4},\ldots)+\cdots$,
by differentiation. The equations $k_{1}+k_{2}+\cdots= j$ and $k_{1}+2k_{2}+\cdots= n$ are preserved in this induction relationship. We can easily factor $n!/(k_{1}!(1!)^{k_{1}}k_{2}!(2!)^{k_{2}}\ldots)$ out of each term appearing on the right-hand side of the equation for $c(n+1,j,k_{1},\ldots)$, and we are left with $k_{1}+2k_{2}+3k_{3}+\cdots= n+1$. (In the proof it is convenient to assume that there are infinitely many k’s, although clearly $k_{n+1}=k_{n+2}=\cdots=0$.)
The solution just given makes use of standard techniques, but it doesn’t give a satisfactory explanation of why the formula has this form, nor how it could have been discovered in the first place. Let us examine this question using a combinatorial argument suggested by H. S. Wall [Bull. Amer. Math. Soc. 44 (1938), 395–398]. Write for convenience $w_j=D_{u}^{j}w$, $u_k=D_{x}^{k}u$. Then $D_{x}(w_{j})=w_{j+1}u_{1}$ and $D_{x}(u_{k})=u_{k+1}$.
By these two rules and the rule for derivative of a product we find
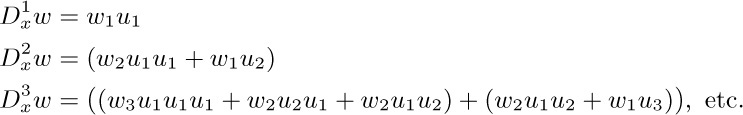
Analogously we may set up a corresponding tableau of set partitions thus:
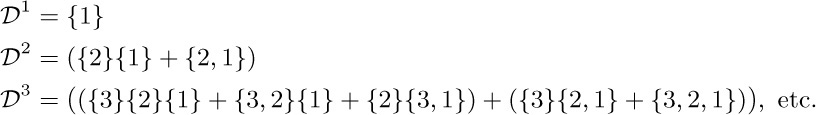
Formally, if $a_{1}a_{2}\ldots a_{j}$ is a partition of the set $\{1,2,\ldots,n-1\}$, define
${\cal D}a_{1}a_{2}\ldots a_{j}=\{n\}a_{1}a_{2}\ldots a_{j}+(a_{1}∪\{n\})a_{2}\ldots a_{j}+$ $a_{1}(a_{2}∪\{n\})\ldots a_{j}+\cdots+a_{1}a_{2}\ldots(a_{j}∪\{n\})$.
This rule is an exact parallel of the rule
$D_{x}(w_{j}u_{r_{1}}u_{r_{2}}\ldots u_{r_{j}})=w_{j+1}u_{1}u_{r_{1}}u_{r_{2}}\ldots u_{r_{j}}+$ $w_{j}u_{r_{1}+1}u_{r_{2}}\ldots u_{r_{j}}+$ $w_{j}u_{r_{1}}u_{r_{2}+1}\ldots u_{r_{j}}+\cdots+w_{j}u_{r_{1}}u_{r_{2}}\ldots u_{r_{j}+1}$,
if we let the term $w_{j}u_{r_{1}}u_{r_{2}}\ldots u_{r_{j}}$ correspond to a partition $a_{1}a_{2}\ldots a_{j}$ with $r_{t}$ elements in $a_{t}$, $1≤t≤j$. So there is a natural mapping from ${\cal D}^{n}$ onto $D_{x}^{n}w$, and furthermore it is easy to see that ${\cal D}^{n}$ includes each partition of the set $\{1,2,\ldots,n\}$ exactly once. (See exercise 1.2.6–64.)
From these observations we find that if we collect like terms in $D_{x}^{n}w$, we obtain a sum of terms $c(k_{1},k_{2},\ldots)w_{j}u_{1}^{k_1}u_{2}^{k_2}\ldots$, where $j=k_{1}+k_{2}+\cdots$ and $n=k_{1}+2k_{2}+\cdots$, and where $c(k_{1},k_{2},\ldots)$ is the number of partitions of $\{1,2,\ldots,n\}$ into j subsets such that there are $k_{t}$ subsets having t elements.
It remains to count these partitions. Consider an array of $k_{t}$ boxes of capacity t:
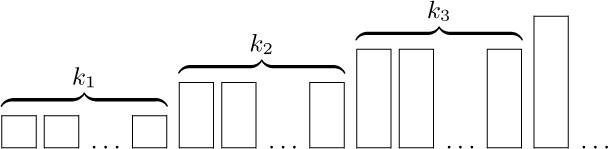
The number of ways to put n different elements into these boxes is the multinomial coefficient
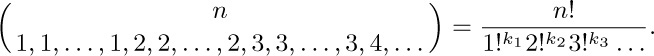
To get $c(k_{1},k_{2},k_{3},\ldots)$ we should divide this by $k_{1}!\,k_{2}!\,k_{3}!\ldots$, since the boxes in each group of $k_{t}$ are indistinguishable from each other; they may be permuted in $k_{t}!$ ways without affecting the set partition.
Arbogast’s original proof [Du Calcul des Dérivations (Strasbourg: 1800), §52] was based on the fact that $D_{x}^{k}u/k!$ is the coefficient of $z^{k}$ in $u(x+z)$ and $D_{u}^{j}w/j!$ is the coefficient of $y^{j}$ in $w(u+y)$, hence the coefficient of $z^{n}$ in $w(u(x+z))$ is
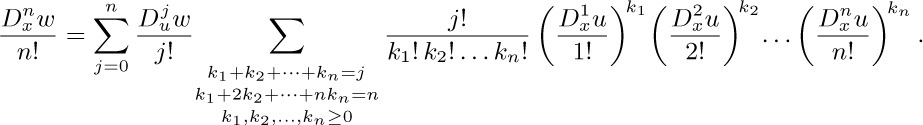
His formula was forgotten for many years, then rediscovered independently by F. Faà di Bruno [Quarterly J. Math. 1 (1857), 359–360], who observed that it can also be expressed as a determinant
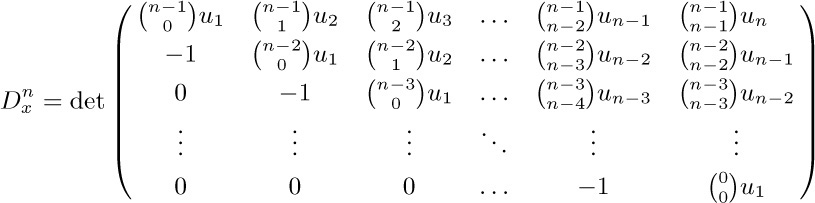
where $u_j=(D_{x}^{j}u)D_{u}$; both sides of this equation are differential operators to be applied to w. For a generalization of Arbogast’s formula to functions of several variables, and a list of references to other related work, see the paper by I. J. Good, Annals of Mathematical Statistics 32 (1961), 540–541.
22. The hypothesis that $\lim_{n→∞}(n+x)!/(n!\,n^{x})=1$ is valid for integers x; for example, if x is positive, the quantity is $(1+1/n)(1+2/n)\ldots(1+x/n)$, which certainly approaches unity. If we also assume that $x!=x(x-1)!$, the hypothesis leads us to conclude immediately that
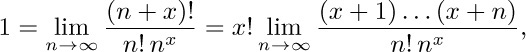
which is equivalent to the definition given in the text.
23. $z(-z)!\,\varGamma(z)=\lim_{m→∞}\prod_{n=1}^{m}(1-z/n)^{-1}(1+z/n)^{-1}$ by (13) and (15).
24. $n^{n}/n!=\prod_{k=1}^{n-1}(k+1)^{k}/k^{k}\le\prod_{k=1}^{n-1}e$; $n!/n^{n+1}=\prod_{k=1}^{n-1}k^{k+1}/(k+1)^{k+1}\le\prod_{k=1}^{n-1}e^{-1}$.
25. $x^{\underline{m+n}}=x^{\underline m}(x-m)^{\underline n}$; $x^{\overline{m+n}}=x^{\overline m}(x+m)^{\overline n}$. These laws hold also when m and n are nonintegers, by (21).
1. n, since each combination leaves out one item.
2. 1. There’s exactly one way to choose nothing from the empty set.
3. $\mybinomf{52}{13}$. The actual number is 635013559600.
4. $2^{4}·5^{2}·7^{2}·17·23·41·43·47$.
5. $(10+1)^{4}=10000+4(1000)+6(100)+4(10)+1$.
6. 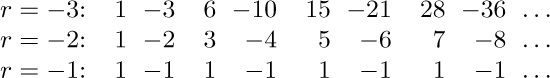
7. $\lfloor{n/2}\rfloor$; or, alternatively, $\lceil{n/2}\rceil$. It is clear from (3) that for smaller values the binomial coefficient is strictly increasing, and afterwards it decreases to zero.
8. The nonzero entries in each row are the same from left to right as from right to left.
9. One if n is positive or zero; zero if n is negative.
10. (a), (b) and (f) follow immediately from (e); (c) and (d) follow from (a), (b), and Eq. (9). Thus it suffices to prove (e). Consider $\mybinomf{n}{k}$ as a fraction, given by Eq. (3) with factors in numerator and denominator. The first $k\bmod p$ factors have no p’s in the denominator, and in the numerator and denominator these terms are clearly congruent to the corresponding terms of
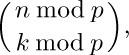
which differ by multiples of p. (When dealing with non-multiples of p we may work modulo p in both numerator and denominator, since if $a≡c$ and $b≡d$ and $a/b$, $c/d$ are integers, then $a/b≡c/d$.) There remain $k-k\bmod p$ factors, which fall into $\lfloor{k/p}\rfloor$ groups of p consecutive values each. Each group contains exactly one multiple of p; the other $p-1$ factors in a group are congruent $(\text{modulo }p)$ to $(p-1)!$ so they cancel in numerator and denominator. It remains to investigate the $\lfloor{k/p}\rfloor$ multiples of p in numerator and denominator; we divide each of them by p and are left with the binomial coefficient
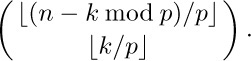
If $k\bmod p≤n\bmod p$, this equals
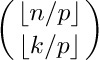
as desired; and if $k\bmod p\gt n\bmod p$, the other factor $\mybinomf{n\bmod p}{k\bmod p}$ is zero, so the formula holds in general. [American J. Math. 1 (1878), 229–230; see also L. E. Dickson, Quart. J. Math. 33 (1902), 383–384; N. J. Fine, AMM 54 (1947), 589–592.]
11. If $a=a_{r}p^{r}+\cdots+a_{0}$, $b=b_{r}p^{r}+\cdots+b_{0}$, and $a+b=c_{r}p^{r}+\cdots+c_{0}$, the value of n (according to exercise 1.2.5–12 and Eq. (5)) is
$(a_{0}+\cdots+a_{r}+b_{0}+\cdots+b_{r}-c_{0}-\cdots-c_{r})/(p-1)$.
A carry decreases $c_{j}$ by p and increases $c_{j+1}$ by 1, giving a net change of +1 in this formula. [Similar results hold for q-nomial and Fibonomial coefficients; see Knuth and Wilf, Crelle 396 (1989), 212–219.]
12. By either of the two previous exercises, n must be one less than a power of 2. More generally, $\mybinomf{n}{k}$ is never divisible by the prime p, $0≤k≤n$, if and only if $n=ap^{m}-1$, $1≤a\lt p$, $m≥0$.
14. $24\mybinomf{n+1}{5}+36\mybinomf{n+1}{4}+14\mybinomf{n+1}{3}+\mybinomf{n+1}{2}=$ $\frac{n^{5}}{5}+\frac{n^{4}}{2}+\frac{n^{3}}{3}-\frac{n}{30}=$ $\frac{n(n+1)(n+\frac12)(3n^{2}+3n-1)}{15}$.
17. We may assume that r and s are positive integers. Also
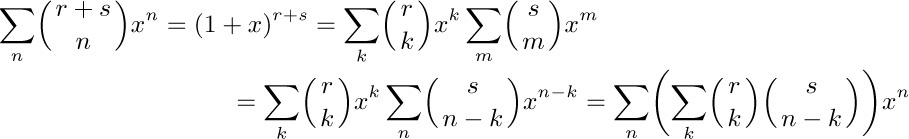
for all x, so the coefficients of $x^{n}$ must be identical.
21. The left-hand side is a polynomial of degree ≤ n; the right-hand side is a polynomial of degree $m+n+1$. The polynomials agree at $n+1$ points, but that isn’t enough to prove them equal. [In fact, the correct formula in general is
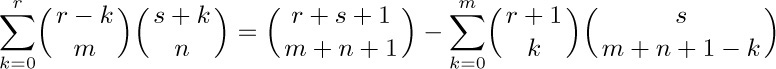
when m, n, and r are nonnegative integers.]
22. Assume that $n\gt 0$. The kth term is $r/(r-tk)$ times
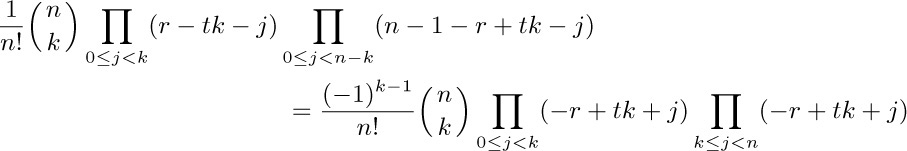
and the two products give a polynomial of degree $n-1$ in k after division by $r-tk$. So the sum over k is zero by Eq. (34).
24. The proof is by induction on n. If n ≤ 0 the identity is obvious. If n > 0, we prove it holds for $(r,n-r+nt+m,t,n)$, by induction on the integer m ≥ 0, using the previous two exercises and the validity for n − 1. This establishes the identity $(r,s,t,n)$ for infinitely many s, and it holds for all s since both sides are polynomials in s.
25. Using the ratio test and straightforward estimates for large values of k we can prove convergence. When w is sufficiently small, we have
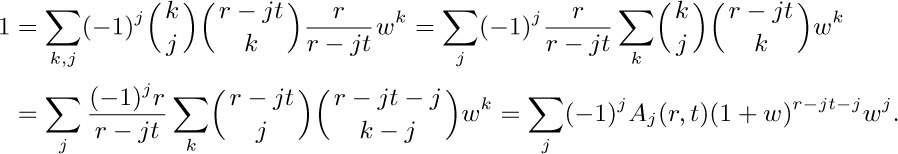
Now let $x=1/(1+w)$, $z=-w/(1+w)^{1+t}$. This proof is due to H. W. Gould [AMM 63 (1956), 84–91]. See also the more general formulas in exercises 2.3.4.4–33 and 4.7–22.
26. We could start with identity (35) in the form
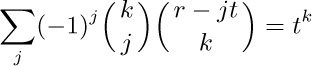
and proceed as in exercise 25. Another way is to differentiate the formula of that exercise with respect to z; we get
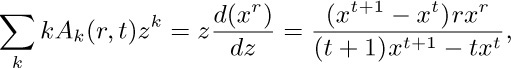
hence we can obtain the value of
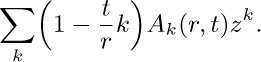
27. For Eq. (26), multiply the series for $x^{r+1}/((t+1)x-t)$ by the series for $x^{s}$, and get a series for $x^{r+s+1}/((t+1)x-t)$ in which coefficients of z may be equated to the coefficients arising from the series for $x^{(r+s)+1}/((t+1)x-t)$.
28. Denoting the left-hand side by $f(r,s,t,n)$, we find
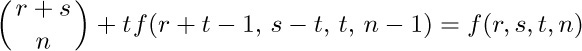
by considering the identity
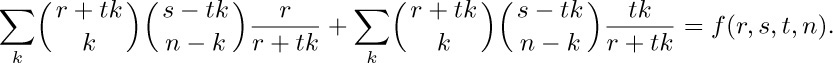
29. $\displaystyle\left.{(-1)^{k}\binom{n}{k}}\middle/{n!}=(-1)^{k}/(k!\,(n-k)!)={(-1)^{n}}\middle/\right.{\prod_{\begin{myarray2}{0\le j\le n\\j\ne k}\end{myarray2}}}(k-j)$.
30. Apply (7), (6), and (19) to get
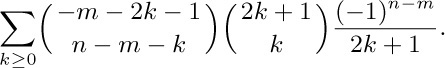
Now we can apply Eq. (26) with $(r,s,t,n)=(1,m-2n-1,-2,n-m)$, obtaining
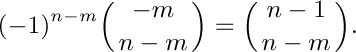
This result is the same as our previous formula, when n is positive, but when n = 0 the answer we have obtained is correct while $\mybinomf{n-1}{m-1}$ is not. Our derivation has a further bonus, since the answer $\mybinomf{n-1}{n-m}$ is valid for n ≥ 0 and all integers m.
31. [This sum was first obtained in closed form by J. F. Pfaff, Nova Acta Acad. Scient. Petr. 11 (1797), 38–57.] We have
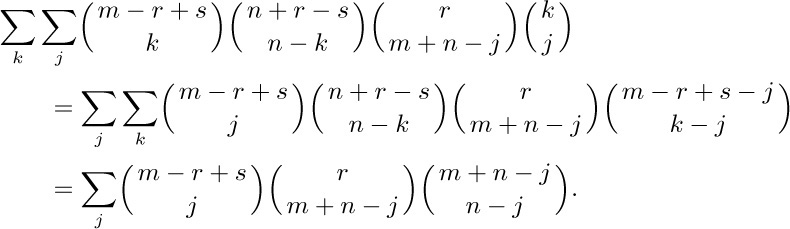
Changing $\mybinomf{m+n-j}{n-j}$ to $\mybinomf{m+n-j}{m}$ and applying (20) again, we get
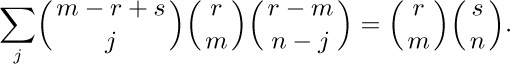
33, 34. [Mém. Acad. Roy. Sci. (Paris, 1772), part 1, 492; C. Kramp, Élémens d’Arithmétique Universelle (Cologne: 1808), 359; Giornale di Mat. Battaglini 33 (1895), 179–182.] Since $x^{\overline n}=n!\,\mybinomf{x+n-1}{n}$, the equation may be transformed into
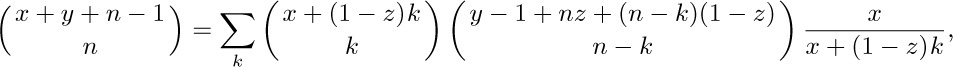
which is a case of (26). Similarly, $(x+y)^{\underline n}=\sum_{k}\mybinomf{n}{k}x(x-kz-1)^{\underline{k-1}}(y+kz)^{\underline{n-k}}$, an equivalent formula of Rothe [Formulæ de Serierum Reversione (Leipzig: 1793), 18].
35. For example, we prove the first formula:
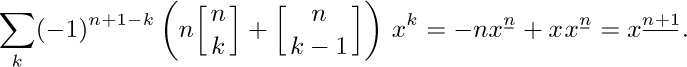
36. By (13), assuming that n is a nonnegative integer, we get $2^{n}$ and $δ_{n0}$, respectively.
37. When $n\gt 0$, $2^{n-1}$. (The odd and even terms cancel, so each equals half the total sum.)
38. Let $ω=e^{2πi/m}$. Then
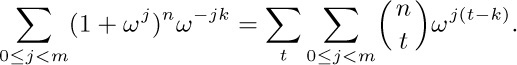
Now
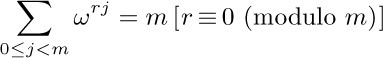
(it is the sum of a geometric progression), so the right-hand sum is $\displaystyle m\sum_{t\bmod m=k}\binom{n}{t}$.
The original sum on the left is
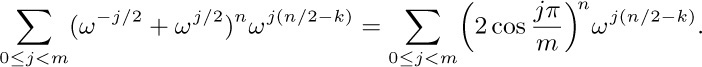
Since the quantity is known to be real, we may take the real part and obtain the stated formula. [See Crelle 11 (1834), 353–355.]
The cases m = 3 and m = 5 have special properties discussed in CMath, exercises 5.75 and 6.57.
39. $n!$; $δ_{n0}-δ_{n1}$. (The row sums in the second triangle are not so simple; we will find (exercise 64) that $\sum_{k}{n\brace k}$ is the number of ways to partition a set of n elements into disjoint sets, which is the number of equivalence relations on $\{1,2,\ldots,n\}$.)
40. Proof of (c): By parts,
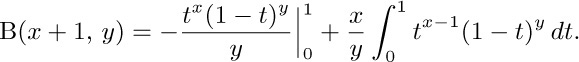
Now use (b).
41. $m^{x}{\rm B}(x,m+1)→\varGamma(x)$ as $m→∞$, regardless of whether m runs through integer values or not (by monotonicity). Hence, $(m+y)^{x}{\rm B}(x,m+y+1)→\varGamma(x)$, and $(m/(m+y))^{x}→1$.
42. $1/((r+1){\rm B}(k+1,r-k+1))$, if this is defined according to exercise 41(b). In general when z and w are arbitrary complex numbers we define
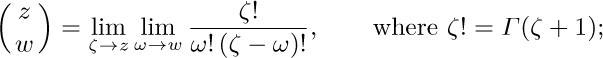
the value is infinite when z is a negative integer and w is not an integer.
With this definition, the symmetry condition (6) holds for all complex n and k, except when n is a negative integer and k is an integer; Eqs. (7), (9), and (20) are never false, although they may occasionally take indeterminate forms such as $0·∞$ or $∞+∞$. Equation (17) becomes
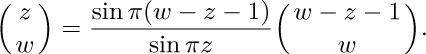
We can even extend the binomial theorem (13) and Vandermonde’s convolution (21), obtaining $\sum_{k}\mybinomf{r}{\alpha+k}z^{\alpha+k}=(1+z)^{r}$ and $\sum_{k}\mybinomf{r}{\alpha+k}\mybinomf{s}{\beta-k}=\mybinomf{r+s}{\alpha+\beta}$; these formulas hold for all complex r, s, z, α, and β whenever the series converge, provided that complex powers are suitably defined. [See L. Ramshaw, Inf. Proc. Letters 6 (1977), 223–226.]
43. $\int_{0}^{1}dt/(t^{1/2}(1-t)^{1/2})=2\int_{0}^{1}du/(1-u^{2})^{1/2}=$ $2\arcsin u{\atopwithdelims.|}_0^1=\pi$.
45. For large r, $\displaystyle\frac{1}{k\varGamma(k)}\sqrt{\frac{r}{r-k}}\frac{1}{e^k}\frac{(1-k/r)^k}{(1-k/r)^r}\to\frac{1}{\varGamma(k+1)}$.
46. $\displaystyle\sqrt{\frac{1}{2\pi}\left(\frac{1}{x}+\frac{1}{y}\right)}\left(1+\frac{y}{x}\right)^{x}\left(1+\frac{x}{y}\right)^{y}$, and $\displaystyle\binom{2n}{n}\approx4^{n}/\sqrt{\pi n}$.
47. Each quantity is $δ_{k0}$ when $k≤0$, and is multiplied by $(r-k)(r-\frac12-k)/(k+1)^2$ when k is replaced by $k+1$. When $r=-\frac12$ this implies $\mybinomf{-1/2}{k}=(-1/4)^{k}\mybinomf{2k}{k}$.
48. This can be proved by induction, using the fact that
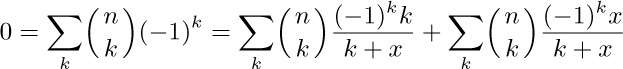
when $n\gt 0$. Alternatively, we have
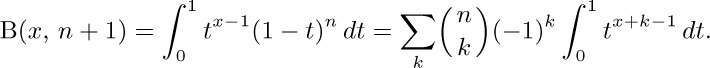
(In fact, the stated sum equals ${\rm B}(x,n+1)$ for noninteger n also, when the series converges.)
49. $\displaystyle\binom{r}{m}=\sum_{k}{\binom{r}{k}}{\binom{-r}{m-2k}}(-1)^{m+k}$, integer m. (See exercise 17.)
50. The kth summand is $\mybinomf{n}{k}(-1)^{n-k}(x-kz)^{n-1}x$. Apply Eq. (34).
51. The right-hand side is
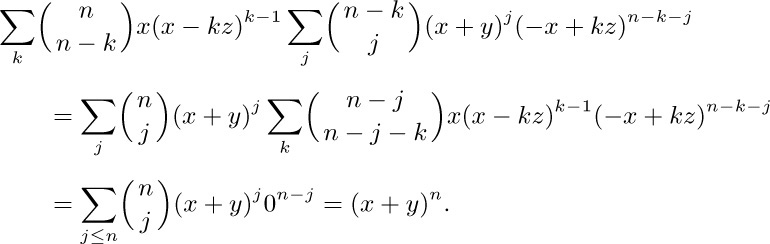
The same device may be used to prove Torelli’s sum (exercise 34).
Another neat proof of Abel’s formula comes from the fact that it is readily transformed into the more symmetric identity derived in exercise 2.3.4.4–29:
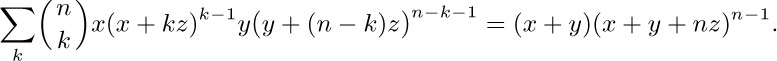
Abel’s theorem has been generalized even further by A. Hurwitz [Acta Mathematica 26 (1902), 199–203] as follows:
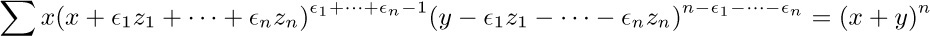
where the sum is over all $2^{n}$ choices of $\epsilon_{1},\ldots,\epsilon_{n}=\rm0\;or\;1$ independently. This is an identity in $x,y,z_{1},\ldots,z_{n}$, and Abel’s formula is the special case $z_{1}=z_{2}=\cdots=z_{n}$. Hurwitz’s formula follows from the result in exercise 2.3.4.4–30.
52. $∑_{k≥0}(k+1)^{-2}=π^{2}/6$. [M. L. J. Hautus observes that the sum is absolutely convergent for all complex x, y, z, n whenever $z≠0$, since the terms for large k are always of order $1/k^{2}$. This convergence is uniform in bounded regions, so we may differentiate the series term by term. If $f(x,y,n)$ is the value of the sum when $z=1$, we find $(∂/∂y)f(x,y,n)=nf(x,y,n-1)$ and $(∂/∂x)f(x,y,n)=nf(x-1,y+1,n-1)$. These formulas are consistent with $f(x,y,n)=(x+y)^{n}$; but actually the latter equality seems to hold rarely, if ever, unless the sum is finite. Furthermore the derivative with respect to z is almost always nonzero.]
53. For (b), set $r=\frac12$ and $s=-\frac12$ in the result of (a).
54. Insert minus signs in a checkerboard pattern as shown.
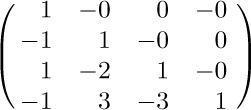
This is equivalent to multiplying $a_{ij}$ by $(-1)^{i+j}$. The result is the desired inverse, by Eq. (33).
55. Insert minus signs in one triangle, as in the previous exercise, to get the inverse of the other. (Eq. (47).)
56. 210 310 320 321 410 420 421 430 431 432 510 520 521 530 531 532 540 541 542 543 610. With a fixed, b and c run through the combinations of a things two at a time; with a and b fixed, c runs through the combinations of b things one at a time.
Similarly, we could express all numbers in the form $n=\mybinomf{a}{4}+\mybinomf{b}{3}+\mybinomf{c}{2}+\mybinomf{d}{1}$ with $a\gt b\gt c\gt d ≥ 0$; the sequence begins 3210 4210 4310 4320 4321 5210 5310 5320 … . We can find the combinatorial representation by a “greedy” method, first choosing the largest possible a, then the largest possible b for $n-\mybinomf{a}{4}$, etc. [Section 7.2.1.3 discusses further properties of this representation.]
58. [Systematisches Lehrbuch der Arithmetik (Leipzig: 1811), xxix.] Use induction and
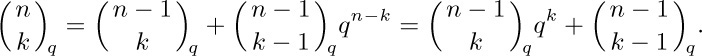
Therefore [F. Schweins, Analysis (Heidelberg: 1820),§151] the q-generalization of (21) is
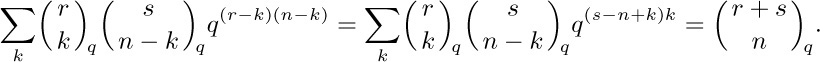
And the identity $1-q^{t}=-q^{t}(1-q^{-t})$ makes it easy to generalize (17) to
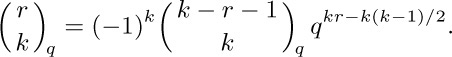
The q-nomial coefficients arise in many diverse applications; see, for example, Section 5.1.2, and the author’s note in J. Combinatorial Theory A10 (1971), 178–180.
Useful facts: When n is a nonnegative integer, $\mybinomf{n}{k}_q$ is a polynomial of degree $k(n-k)$ in q with nonnegative integer coefficients, and it satisfies the reflective laws
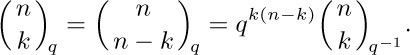
If $|q|\lt 1$ and $|x|\lt 1$, the q-nomial theorem holds when n is an arbitrary real number, if we replace the left-hand side by $∏_{k≥0}((1+q^{k}x)/(1+q^{n+k}x))$. Properties of power series make it necessary to verify this only when n is a positive integer, because we can set $q^{n}=y$; the identity has then been verified for infinitely many values of y. Now we can negate the upper index in the q-nomial theorem, obtaining
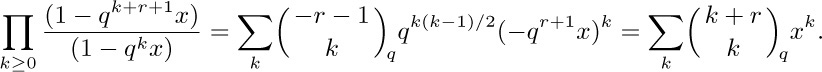
For further information, see G. Gasper and M. Rahman, Basic Hypergeometric Series (Cambridge Univ. Press, 1990). The q-nomial coefficients were introduced by Gauss in Commentationes societatis regiæ scientiarum Gottingensis recentiores 1 (1808), 147– 186; see also Cauchy [Comptes Rendus Acad. Sci. 17 (Paris, 1843), 523–531], Jacobi [Crelle 32 (1846), 197–204], Heine [Crelle 34 (1847), 285–328], and Section 7.2.1.4.
59. $(n+1)\mybinomf{n}{k}-\mybinomf{n}{k+1}$.
60. $\displaystyle\binom{n+k-1}{k}$. This formula can be remembered easily, since it is
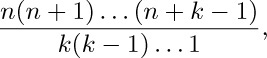
like Eq. (2) except that the numbers in the numerator go up instead of down. A slick way to prove it is to note that we want to count the number of integer solutions $(a_{1},\ldots,a_{k})$ to the relations $1≤a_{1}≤a_{2}≤\cdots≤a_{k}≤n$. This is the same as $0\lt a_{1}\lt a_{2}+1\lt\cdots\lt a_{k}+k-1\lt n+k$; and the number of solutions to
$0\lt b_{1}\lt b_{2}\lt\cdots\lt b_{k}\lt n+k$
is the number of choices of k distinct things from the set $\{1,2,\ldots,n+k-1\}$. (This trick is due to H. F. Scherk, Crelle 3 (1828), 97; curiously it was also given by W. A. Förstemann in the same journal, 13 (1835), 237, who said “One would almost believe this must have been known long ago, but I have found it nowhere, even though I have consulted many works in this regard.”)
61. If $a_{mn}$ is the desired quantity, we have $a_{mn}=na_{m(n-1)}+δ_{mn}$ by (46) and (47). Hence the answer is $[n≥m]\,n!/m!$. The same formula is also easily obtained by inversion of (56).
62. Use the identity of exercise 31, with $(m,n,r,s,k)←(m+k,l-k,m+n,n+l,j)$:
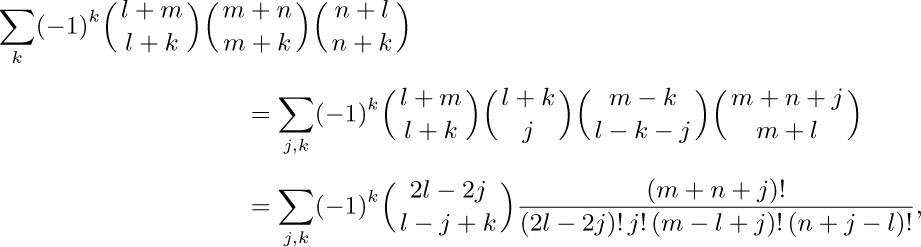
by rearranging the factorial signs. The sum on k now vanishes unless $j=l$.
The case $l=m=n$ of this identity was published by A. C. Dixon [Messenger of Math. 20 (1891), 79–80], who established the general case twelve years later [Proc. London Math. Soc. 35 (1903), 285–289]. However, L. J. Rogers had already published a much more general formula in the meantime [Proc. London Math. Soc. 26 (1895), 15–32,§8]. See also papers by P. A. MacMahon, Quarterly Journal of Pure and Applied Math. 33 (1902), 274–288, and John Dougall, Proc. Edinburgh Math. Society 25 (1907), 114–132. The corresponding q-nomial identities are
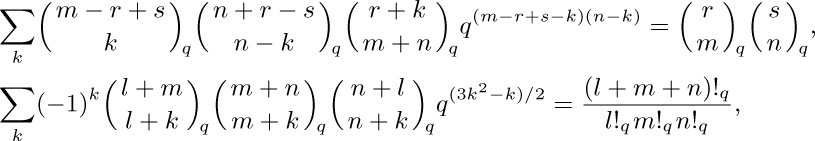
where $n!_q=\prod_{k=1}^{n}(1+q+\cdots+q^{k-1})$.
63. See CMath, exercises 5.83 and 5.106.
64. Let $f(n,m)$ be the number of partitions of $\{1,2,\ldots,n\}$ into m parts. Clearly $f(1,m)=δ_{1m}$. If $n\gt 1$, the partitionings are of two varieties: (a) The element n alone forms a set of the partition; there are $f(n-1,m-1)$ ways to construct partitions like this. (b) The element n appears together with another element; there are m ways to insert n into any m-partition of $\{1,2,\ldots,n-1\}$, hence there are $mf(n-1,m)$ ways to construct partitions like this. We conclude that $f(n,m)=f(n-1,m-1)+mf(n-1,m)$, and $f(n,m)={n\brace m}$ by induction.
65. See AMM 99 (1992), 410–422.
66. Let $X=\mybinomf{x}{n}$, $\underline{X}=\mybinomf{x}{n-1}=\frac{n}{x-n+1}X$, $\overline{X}=\mybinomf{x}{n+1}=\frac{x-n}{n+1}X$, with similar notations for Y and Z. We may assume that $y\gt n-1$ is fixed, so that x is a function of z.
Let $F(z)=\overline{X}-\overline{Y}-\overline{Z}$, and suppose that $F(z)=0$ for some $z\gt n-2$. We will prove that $F'(z)\lt0$; therefore $z=y$ must be the only root $\gt n-2$, proving the second inequality. Since $F(z)=\frac{x-n}{n+1}(Y+Z)-\frac{y-n}{n+1}Y-\frac{z-n+1}{n}Z=0$ and $x\gt y$ and $Y,Z\gt 0$, we must have $\frac{x-n}{n+1}\lt\frac{z-n+1}{n}$. Setting $X'=dX/dx$ and $Z'=dZ/dz=dX/dz$, we have
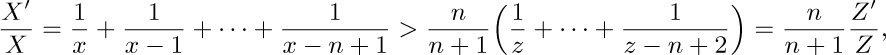
since $\frac{x-n+1}{n+1}\lt\frac{z-n+2}{n},\cdots,\frac{x-1}{n+1}\lt\frac{z}{n}$. Thus $dx/dz=Z'/X'\lt\frac{n+1}{n}(Z/X)$, and
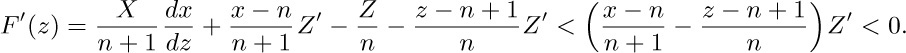
To prove the first inequality, we may assume that $n\gt 2$. Then if $\underline{X}=\underline{Y}+\underline{Z}$ for some $z\gt n-2$, the second inequality tells us that $z=y$.
References: L. Lovász, Combinatorial Problems and Exercises (1993), Problem 13.31(a); R. M. Redheffer, AMM 103 (1996), 62–64.
67. If k > 0, exercise 1.2.5–24 gives the slightly sharper (but less memorable) upper bounds $\mybinomf{n}{k}=n^{\underline{k}}/k!\le n^{k}/k!\le\frac{1}{e}(\frac{ne}{k})^{k}\le(\frac{ne}{k+1})^{k}$. The corresponding lower bound is $\mybinomf{n}{k}\ge{\big(}\frac{(n-k+1)e}{k}{\big)}^{k}\frac{1}{ek}$, which is less memorable (but often sharper) than $\mybinomf{n}{k}\ge(\frac{n}{k})^{k}$.
68. Let $t_k=k\mybinomf{n}{k}p^{k}(1-p)^{n+1-k}$; then $t_{k}-t_{k+1}=\mybinomf{n}{k}p^{k}(1-p)^{n-k}(k-np)$. So the stated sum is
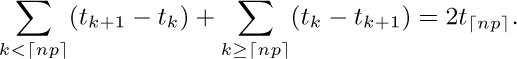
[De Moivre stated this identity in Miscellanea Analytica (1730), 101, in the case that np is an integer; H. Poincaré proved the general case in his Calcul des Probabilités (1896), 56–60. See P. Diaconis and S. Zabell, Statistical Science 6 (1991), 284–302, for the interesting history of this identity and for a variety of similar formulas.]
1. 0, 1, and $3/2$.
2. Replace each term $1/(2^{m}+k)$ by the upper bound $1/2^{m}$.
3. $H_{2^{m}-1}^{(r)}\le\sum_{0\le k\lt m}2^{k}/2^{kr}$; $2^{r-1}/(2^{r-1}-1)$ is an upper bound.
4. (b) and (c).
5. 9.78760 60360 44382 …
6. Induction and Eq. 1.2.6–(46).
7. $T(m+1,n)-T(m,n)=$ $1/(m+1)-1/(mn+1)-\cdots-1/(mn+n)≤$ $1/(m+1)-(1/(mn+n)+\cdots+1/(mn+n))=$ $1/(m+1)-n/(mn+n)=0$. The maximum value occurs at $m=n=1$, and the minimum is approached when m and n get very large. By Eq. (3) the greatest lower bound is γ, which is never actually attained. A generalization of this result appears in AMM 70 (1963), 575–577.
8. By Stirling’s approximation, $\ln n!$ is approximately $(n+\frac12)\ln n-n+\ln\sqrt{2\pi}$; also $\sum_{k=1}^{n}H_{k}$ is approximately $(n+1)\ln n-n(1-\gamma)+(\gamma+\frac12)$; the difference is approximately $\gamma n+\frac{1}{2}\ln n+.158$.
9. $-1/n$.
10. Break the left side into two sums; change k to k + 1 in the second sum.
11. $2-H_{n}/n-1/n$, for $n\gt 0$.
12. 1.000… is correct to more than three hundred decimal places.
13. Use induction as in the proof of Theorem A. Or use calculus: Differentiate with respect to x, also evaluate at $x=1$.
14. See Section 1.2.3, Example 2. The second sum is ${\frac12}{(H_{n+1}^{2}-H_{n+1}^{(2)})}$.
15. $\sum_{j=1}^{n}(1/j)\sum_{k=j}^{n}H_{k}$ can be summed by formulas in the text; the answer comes to $(n+1)H_{n}^{2}-(2n+1)H_{n}+2n$.
16. $H_{2n-1}-\frac{1}{2}H_{n-1}$.
17. First solution (elementary): Taking the denominator to be $(p-1)!$, which is a multiple of the true denominator but not a multiple of p, we must show only that the corresponding numerator, $(p-1)!/1+(p-1)!/2+$ $\cdots+(p-1)!/(p-1)$, is a multiple of p. Modulo p, $(p-1)!/k≡(p-1)!\,k'$, where $k'$ can be determined by the relation $kk'\bmod p=1$. The set $\{1',2',\ldots,(p-1)'\}$ is just the set $\{1,2,\ldots,p-1\}$; so the numerator is congruent to $(p-1)!\,(1+2+\cdots+p-1)≡0$.
Second solution (advanced): By exercise 4.6.2–6, we have $x^{\overline p}≡x^{p}-\md[x]{p}$; hence ${p\brack k}\equiv\delta_{kp}-\delta_{k1}$, by exercise 1.2.6–32. Now apply exercise 6.
The numerator of $H_{p-1}$ is in fact known to be a multiple of $p^{2}$ when $p\gt 3$; see Hardy and Wright, An Introduction to the Theory of Numbers, Section 7.8.
18. If $n=2^{k}m$ where m is odd, the sum equals $2^{2k}m_{1}/m_{2}$ where $m_{1}$ and $m_{2}$ are both odd. [AMM 67 (1960), 924–925.]
19. Only $n=0$, $n=1$. For $n≥2$, let $k=\lfloor{\lg n}\rfloor$. There is precisely one term whose denominator is $2^{k}$, so $2^{k-1}H_{n}-\frac12$ is a sum of terms involving only odd primes in the denominator. If $H_{n}$ were an integer, $2^{k-1}H_{n}-\frac12$ would have a denominator equal to 2.
20. Expand the integrand term by term. See also AMM 69 (1962), 239, and an article by H. W. Gould, Mathematics Magazine 34 (1961), 317–321.
21. $H_{n+1}^{2}-H_{n+1}^{(2)}$.
22. $(n+1)(H_n^{2}-H_n^{(2)})-2n(H_{n}-1)$.
23. $\varGamma'(n+1)/\varGamma(n+1)=1/n+\varGamma'(n)/\varGamma(n)$, since $\varGamma(x+1)=x\varGamma(x)$. Hence $H_{n}=γ+\varGamma'(n+1)/\varGamma(n+1)$. The function $\psi(x)=\varGamma'(x)/\varGamma(x)=H_{x-1}-γ$ is called the psi function or the digamma function. Some values for rational x appear in Appendix A.
24. It is
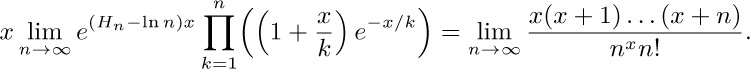
Note: The generalization of $H_{n}$ considered in the previous exercise is therefore equal to $H_{x}^{(r)}=\sum_{k\ge0}(1/(k+1)^{r}-1/(k+1+x)^{r})$, when $r=1$; the same idea can be used for larger values of r. The infinite product converges for all complex x.
25. $H_{n}^{(0,v)}=\sum_{k=1}^{n}H_{n}^{(v)}$ and $H_{n}^{(u,0)}=H_{n}^{(u-1)}$; so the identity generalizes (8). [See L. Euler, Novi Comment. Acad. Sci. Pet. 20 (1775), 140–186,§2.]
1. After k months there are $F_{k+2}$ pairs, so the answer is $F_{14}=377$ pairs.
2. $\ln(\phi^{1000}/\sqrt{5})=1000\ln\phi-\frac{1}{2}\ln 5=480.40711$; $\log_{10}F_{1000}$ is $1/(\ln 10)$ times this, or 208.64; $F_{1000}$ is therefore a 209-digit number whose leading digit is 4.
4. 0, 1, 5; afterwards $F_{n}$ increases too fast.
5. 0, 1, 12.
6. Induction. (The equation holds for negative n also; see exercise 8.)
7. If d is a proper divisor of n, $F_{d}$ divides $F_{n}$. Now $F_{d}$ is greater than one and less than $F_{n}$ provided d is greater than 2. The only nonprime number that has no proper factor greater than 2 is $n=4$; $F_{4}=3$ is the only exception.
8. $F_{-1}=1$; $F_{-2}=-1$; $F_{-n}=(-1)^{n+1}F_{n}$ by induction on n.
9. Not (15). The others are valid, by an inductive argument that proves something true for $n-1$ assuming it true for n and greater.
10. When n is even, it is greater; when n is odd, it is less. (See Eq. (14).)
11. Induction; see exercise 9. This is a special case of exercise 13(a).
12. If ${\cal G}(z)=\sum{\cal F}_{n}z^{n}$, $(1-z-z^{2}){\cal G}(z)=z+F_{0}z^{2}+F_{1}z^{3}+\cdots=z+z^{2}G(z)$. Hence ${\cal G}(z)=G(z)+zG(z)^{2}$; from Eq. (17) we find ${\cal F}_n=((3n+3)/5)F_{n}-(n/5)F_{n+1}$.
13. (a) $a_{n}=rF_{n-1}+sF_{n}$.
(b) Since $(b_{n+2}+c)=(b_{n+1}+c)+(b_{n}+c)$, we may consider the new sequence $b'_{n}=b_{n}+c$. Applying part (a) to $b'_{n}$, we obtain the answer $cF_{n-1}+(c+1)F_{n}-c$.
14. $a_n=F_{m+n+1}+F_{n}-\mybinomf{n}{m}$ $-\mybinomf{n+1}{m-1}-\cdots-\mybinomf{n+m}{0}$.
15. $c_{n}=xa_{n}+yb_{n}+(1-x-y)F_{n}$.
16. $F_{n+1}$. Induction, and $\mybinomf{n+1-k}{k}=\mybinomf{n-k}{k}+\mybinomf{(n-1)-(k-1)}{k-1}$.
17. In general, the quantity $(x^{n+k}-y^{n+k})(x^{m-k}-y^{m-k})-$ $(x^{n}-y^{n})(x^{m}-y^{m})$ is equal to $(xy)^{n}(x^{m-n-k}-y^{m-n-k})(x^{k}-y^{k})$. Set $x=\phi$, $y=\phihat$, and divide by $(\sqrt{5})^{2}$.
18. It is $F_{2n+1}$.
19. Let $u=\cos 72^{°}$, $v=\cos 36^{°}$. We have $u=2v^{2}-1$; $v=1-2\sin^{2}18^{°}=1-2u^{2}$. Hence $u+v=2(v^{2}-u^{2})$, i.e., $1=2(v-u)=2v-4v^{2}+2$. We conclude that $v=\frac{1}{2}\phi$. (Also $u=\frac{1}{2}\phi^{-1}$, $\sin 36^{°}=\frac12 5^{1/4}\phi^{-1/2}$, $\sin 72^{°}=\frac12 5^{1/4}\phi^{1/2}$. Another interesting angle is $α=\arctan\phi=\frac{\pi}{4}+\frac12\arctan\frac12$, for which we have $\sin α=5^{-1/4}\phi^{1/2}$, $\cos α=5^{-1/4}\phi^{-1/2}$.)
20. $F_{n+2}-1$.
21. Multiply by $x^{2}+x-1$; the solution is $(x^{n+1}F_{n+1}+x^{n+2}F_{n}-x)/(x^{2}+x-1)$. If the denominator is zero, x is $1/\phi$ or $1/\phihat$; then the solution is $(n+1-x^{n}F_{n+1})/(2x+1)$.
22. $F_{m+2n}$; set $t=2$ in the next exercise.
23. $\displaystyle\frac{1}{\sqrt{5}}\sum_{k}\binom{n}{k}(\phi^{k}F_{t}^{k}F_{t-1}^{n-k}\phi^{m}-\phihat^{\,k}F_{t}^{k}F_{t-1}^{n-k}\phihat^{\,m})=$ $\displaystyle\frac{1}{\sqrt{5}}(\phi^{m}(\phi F_{t}+F_{t-1})^{n}-\phihat^{\,m}(\phihat F_{t}+F_{t-1})^{n})=$ $\displaystyle F_{m+tn}$.
24. $F_{n+1}$ (expand by cofactors in the first row).
25. $2^{n}\sqrt{5}F_{n}=(1+\sqrt{5})^{n}-(1-\sqrt{5})^{n}$.
26. By Fermat’s theorem, $2^{p-1}≡1$; now apply the previous exercise and exercise 1.2.6–10(b).
27. The statement is true if $p=2$. Otherwise $F_{p-1}F_{p+1}-F_{p}^{2}=-1$; hence, from the previous exercise and Fermat’s theorem, $F_{p-1}F_{p+1}≡\md[0]{p}$. Only one of these factors can be a multiple of p, since $F_{p+1}=F_{p}+F_{p-1}$.
28. $\phihat^{\,n}$. Note: The solution to the recurrence $a_{n+1}=Aa_{n}+B^{n}$, $a_{0}=0$, is
$a_{n}=(A^{n}-B^{n})/(A-B){\rm\;if}\;A≠B,$ $a_{n}=nA^{n-1}{\rm\;if}\;A=B$.
29. (a) 
(b) follows from (6). [É. Lucas, Amer. J. Math. 1 (1878), 201–204.]
30. We argue by induction on m, the statement being obvious when $m=1$:
(a) $\displaystyle\sum_{k}\binom{m}{k}_{\!\!\cal F}(-1)^{\lceil{(m-k)/2}\rceil}F_{n+k}^{m-2}F_{k}=$ $\displaystyle F_{m}\sum_{k}\binom{m-1}{k-1}_{\!\!\cal F}(-1)^{\lceil{(m-k)/2}\rceil}F_{n+k}^{m-2}=0$.
(b) $\displaystyle\sum_{k}\binom{m}{k}_{\!\!\cal F}(-1)^{\lceil{(m-k)/2}\rceil}F_{n+k}^{m-2}(-1)^{k}F_{m-k}=$ $\displaystyle(-1)^{m}F_{m}\sum_{k}\binom{m-1}{k}_{\!\!\cal F}(-1)^{\lceil{(m-1-k)/2}\rceil}F_{n+k}^{m-2}=0$.
(c) Since $(-1)^{k}F_{m-k}=F_{k-1}F_{m}-F_{k}F_{m-1}$ and $F_{m}≠0$, we conclude from (a) and (b) that $\sum_{k}\mybinomf{m}{k}_{\!\cal F}(-1)^{\lceil{(m-k)/2}\rceil}F_{n+k}^{m-2}F_{k-1}=0$.
(d) Since $F_{n+k}=F_{k-1}F_{n}+F_{k}F_{n+1}$ the result follows from (a) and (c). This result may also be proved in slightly more general form by using the q-nomial theorem of exercise 1.2.6–58. References: Dov Jarden, Recurring Sequences, 2nd ed. (Jerusalem, 1966), 30–33; J. Riordan, Duke Math. J. 29 (1962), 5–12.
31. Use exercises 8 and 11.
32. Modulo $F_{n}$ the Fibonacci sequence is $0,1,\ldots,F_{n-1},0,F_{n-1},-F_{n-2},\ldots$.
33. Note that $\cos z=\frac12 (e^{iz}+e^{-iz})=-i/2$, for this particular z; then use the fact that $\sin(n+1)z+\sin(n-1)z=2\sin nz\cos z$, for all z.
34. Prove that the only possible value for $F_{k_{1}}$ is the largest Fibonacci number less than or equal to n; hence $n-F_{k_{1}}$ is less than $F_{k_{1}-1}$, and by induction there is a unique representation of $n-F_{k_{1}}$. The outline of this proof is quite similar to the proof of the unique factorization theorem. The Fibonacci number system is due to E. Zeckendorf [see Simon Stevin 29 (1952), 190–195; Bull. Soc. Royale des Sciences de Liège 41 (1972), 179–182]; but Section 7.2.1.7 points out that it was implicitly known in 14th-century India. Generalizations are discussed in exercise 5.4.2–10 and in Section 7.1.3.
35. See G. M. Bergman, Mathematics Magazine 31 (1957), 98–110. To represent $x\gt 0$, find the largest k with $\phi^{k}≤x$ and represent x as $\phi^{k}$ plus the representation of $x-\phi^{k}$.
The representation of nonnegative integers can also be obtained from the following all-integer recursive rules, starting with the trivial representations of 0 and 1: Let $L_{n}=\phi^{n}+\phihat^{\,n}=F_{n+1}+F_{n-1}$. The representation of $L_{2n}+m$ for $0≤m≤L_{2n-1}$ and $n≥1$ is $\phi^{2n}+\phi^{-2n}$ plus the representation of m. The representation of $L_{2n+1}+m$ for $0\lt m\lt L_{2n}$ and $n≥0$ is $\phi^{2n+1}+\phi^{-2n-2}$ plus the representation of $m-\phi^{-2n}$, where the latter is obtained by applying the rule $\phi^{k}-\phi^{k-2j}=$ $\phi^{k-1}+\phi^{k-3}+\cdots+\phi^{k-2j+1}$. It turns out that all strings α of 0s and 1s, such that α begins with 1 and has no adjacent 1s, occur to the left of the radix point in the representation of exactly one positive integer, except for the strings that end with $10^{2k}1$; the latter strings never occur in such representations.
36. We may consider the infinite string $S_{∞}$, since $S_{n}$ for $n\gt 1$ consists of the first $F_{n}$ letters of $S_{∞}$. There are no double a’s, no triple b’s. The string $S_{n}$ contains $F_{n-2}$ a’s and $F_{n−1}$ b’s. If we express $m-1$ in the Fibonacci number system as in exercise 34, the mth letter of $S_{∞}$ is a if and only if $k_{r}=2$. The kth letter of $S_{∞}$ is b if and only if $\lfloor{(k+1)\phi^{-1}}\rfloor-\lfloor{k\phi^{-1}}\rfloor=1$; the number of b’s in the first k letters is therefore $\lfloor{(k+1)\phi^{-1}}\rfloor$. Also, the kth letter is b if and only if $k=\lfloor{m\phi}\rfloor$ for some positive integer m. This sequence was studied by John Bernoulli III in the 18th century, by A. A. Markov in the 19th, and by many other mathematicians since then; see K. B. Stolarsky, Canadian Math. Bull. 19 (1976), 473–482.
37. [Fibonacci Quarterly 1 (December 1963), 9–12.] Consider the Fibonacci number system of exercise 34; if $n=F_{k_{1}}+\cdots+F_{k_{r}}\gt 0$ in that system, let $μ(n)=F_{k_{r}}$. Also let $μ(0)=∞$. We find that: (A) If $n\gt 0$, $μ(n-μ(n))\gt 2μ(n)$. Proof: $μ(n-μ(n))=F_{k_{r-1}}≥F_{k_{r}+2}\gt 2F_{k_{r}}$ since $k_{r}≥2$. (B) If $0\lt m\lt F_{k}$, $μ(m)≤2(F_{k}-m)$. Proof: Let $μ(m)=F_j$; $m\le F_{k-1}+F_{k-3}+\cdots+$ $F_{j+(k-1-j)\bmod 2}=-F_{j-1+(k-1-j)\bmod 2}+$ $F_{k}\le-\frac{1}{2}F_{j}+F_{k}$. (C) If $0\lt m\lt μ(n)$, $μ(n-μ(n)+m)≤2(μ(n)-m)$. Proof: This follows from (B). (D) If $0\lt m\lt μ(n)$, $μ(n-m)≤2m$. Proof: Set $m=μ(n)-m$ in (C).
Now we will prove that if there are n chips, and if at most q may be taken in the next turn, there is a winning move if and only if $μ(n)≤q$. Proof: (a) If $μ(n)\gt q$ all moves leave a position n′, q′ with $μ(n')≤q'$. [This follows from (D), above.] (b) If $μ(n)≤q$, we can either win on this move (if $q≥n$) or we can make a move that leaves a position n′, q′ with $μ(n')\gt q'$. [This follows from (A) above: Our move is to take $μ(n)$ chips.] It can be seen that the set of all winning moves, if $n=F_{k_{1}}+\cdots+F_{k_{r}}$, is to remove $F_{k_{j}}+\cdots+F_{k_{r}}$, for some j with $1≤j≤r$, provided that $j=1$ or $F_{k_{j-1}}\gt 2(F_{k_{j}}+\cdots+F_{k_{r}})$.
The Fibonacci representation of 1000 is 987+13; the only lucky move to force a victory is to take 13 chips. The first player can always win unless n is a Fibonacci number.
The solution to considerably more general games of this type has been obtained by A. Schwenk [Fibonacci Quarterly 8 (1970), 225–234].
39. $(3^{n}-(-2)^{n}) /5$.
40. We prove, by induction on m, that $f(n)=m$ for $F_{m}\lt n≤F_{m+1}$: First, $f(n)≤\max(1+f(F_{m})$, $2+f(n-F_{m}))=m$. Second, if $f(n)\lt m$ there is some $k\lt n$ with $1+f(k)\lt m$ (hence $k≤F_{m-1}$) and $2+f(n-k)\lt m$ (hence $n-k≤F_{m-2}$); but then $n≤F_{m-1}+F_{m-2}$. [Thus the Fibonacci trees defined in Section 6.2.1 minimize the maximum root-to-leaf cost when a right branch costs twice as much as a left branch.]
41. $F_{k_{1}+1}+\cdots+F_{k_{r}+1}=\phi n+(\phihat^{\,k_{1}}+\cdots+\phihat^{\,k_{r}})$ is an integer, and the parenthesized quantity lies between $\phihat^{\,3}+\phihat^{\,5}+\cdots=\phihat^{\,-1}-1$ and $\phihat^{\,2}+\phihat^{\,4}+\cdots=\phihat^{\,-1}$. Similarly, $F_{k_{1}-1}+\cdots+F_{k_{r}-1}=\phi^{-1}n+$ $(\phihat^{\,k_{1}}+\cdots+\phihat^{\,k_{r}})=f(\phihat^{\,-1}n)$. [Such Fibonacci shifting is a convenient way to convert mentally between miles and kilometers; see CMath,§6.6.]
42. [Fibonacci Quarterly 6 (1968), 235–244.] If such a representation exists, we have
for all integers N; hence two different representations would contradict exercise 34.
Conversely, we can prove the existence of such joint representations for all nonnegative m and n by induction. But it is more interesting to use the previous exercise, and to prove that such joint representations exist for possibly negative integers m and n if and only if $m+\phi n≥0$: Let N be large enough so that $|m\phihat^{\,N-1}+n\phihat^{\,N}|\lt\phi^{-2}$, and represent $mF_{N-1}+nF_{N}$ as in $(*)$. Then $mF_{N}+nF_{N+1}=\phi(mF_{N-1}+nF_{N})+(m\phihat^{\,N-1}+n\phihat^{\,N})=$ $f(\phi(mF_{N-1}+nF_{N}))=F_{k_{1}+N+1}+\cdots+F_{k_{r}+N+1}$, and it follows that $(*)$ holds for all N. Now set $N=0$ and $N=1$.
1. $1/(1-2z)+1/(1-3z)$.
2. It follows from (6), since $\mybinomf{n}{k}=n!/k!\,(n-k)!$.
3. $G'(z)=\ln(1/(1-z))/(1-z)^{2}+1/(1-z)^{2}$. From this and the significance of $G(z)/(1-z)$, we have $\sum_{k=1}^{n-1}H_{k}=nH_{n}-n$; this agrees with Eq. 1.2.7–(8).
4. Put $t=0$.
5. The coefficient of $z^{k}$ is, by (11) and (22),
Now apply Eqs. 1.2.6–(46) and 1.2.6–(52). (Or, differentiate and use 1.2.6–(46).)
6. $(\ln(1/(1-z)))^{2}$; the derivative is twice the generating function for the harmonic numbers; the sum is therefore $2H_{n−1}/n$.
8. $1/((1-z)(1-z^{2})(1-z^{3})\ldots)$. [This is historically one of the first applications of generating functions. For an interesting account of L. Euler’s eighteenth-century researches concerning this generating function, see G. Pólya, Induction and Analogy in Mathematics (Princeton: Princeton University Press, 1954), Chapter 6.]
9. $\frac{1}{24}S_{1}^{4}+\frac{1}{4}S_{1}^{2}S_{2}+\frac{1}{8}S_{2}^{2}+\frac{1}{3}S_{1}S_{3}+\frac{1}{4}S_{4}$.
10. $G(z)=(1+x_{1}z)\ldots(1+x_{n}z)$. Taking logarithms as in the derivation of Eq. (38), we have the same formulas except that (24) replaces (17), and the answer is exactly the same except that $S_{2},S_{4},S_{6},\ldots$ are replaced by $-S_{2},-S_{4},-S_{6},\ldots$. We have $e_{1}=S_{1}$, $e_{2}=\frac{1}{2}S_{1}^{2}-\frac{1}{2}S_{2}$, $e_{3}=\frac{1}{6}S_{1}^{3}-\frac{1}{2}S_{1}S_{2}+\frac{1}{3}S_{3}$, $e_{4}=\frac{1}{24}S_{1}^{4}-\frac{1}{4}S_{1}^{2}S_{2}+\frac{1}{8}S_{2}^{2}+\frac{1}{3}S_{1}S_{3}-\frac{1}{4}S_{4}$. (See exercise 9.) The recurrence analogous to (39) is $ne_{n}=S_{1}e_{n-1}-S_{2}e_{n-2}+\cdots$.
Note: The equations in this recurrence are called Newton’s identities, since they were first published in Isaac Newton’s Arithmetica Universalis (1707); see D. J. Struik’s Source Book in Mathematics (Harvard University Press, 1969), 94–95.
11. Since $∑_{m≥1}S_{m}z^{m}/m=\ln G(z)=∑_{k≥1}(-1)^{k-1}(h_{1}z+h_{2}z^{2}+\cdots)^{k}/k$, the desired coefficient is $(-1)^{k_{1}+k_{2}+\cdots+k_{m}-1}m(k_{1}+k_{2}+\cdots+k_{m}-1)!/k_{1}!\,k_{2}!\ldots k_{m}!$. [Multiply by $(-1)^{m-1}$ to get the coefficient of $e_{1}^{k_{1}}e_{2}^{k_{2}}\ldots e_{m}^{k_{m}}$ when $S_{m}$ is expressed in terms of the e’s of exercise 10. Albert Girard stated the formulas for $S_{1}$, $S_{2}$, $S_{3}$, and $S_{4}$ in terms of $e_{1}$, $e_{2}$, $e_{3}$, and $e_{4}$ near the end of his Invention Nouvelle en Algébre (Amsterdam: 1629); this was the birth of the theory of symmetric functions.]
12. $\displaystyle\sum_{m,n\ge 0}a_{mn}w^{m}z^{n}=\sum_{m,n\ge 0}\binom{n}{m}w^{m}z^{n}=\sum_{n\ge 0}(1+w)^{n}z^{n}=1/(1-z-wz)$.
13. $\int_{n}^{n+1}e^{-st}f(t)\,dt=(a_{0}+\cdots+a_{n})(e^{-sn}-e^{-s(n+1)})/s$. Adding these expressions together for all n, we find $\class{st}{\rm L}f(s)=G(e^{-s})/s$.
14. See exercise 1.2.6–38.
15. $G_{n}(z)=G_{n-1}(z)+zG_{n-2}(z)+δ_{n0}$, so we find $H(w)=1/(1-w-zw^{2})$. Hence, ultimately, we find
16. $G_{nr}(z)=(1+z+\cdots+z^{r})=\left(\frac{1-z^{r+1}}{1-z}\right)^{n}$.[Note the case $r=∞$.]
17. $\displaystyle\sum_{k}\binom{-w}{k}(-z)^{k}=\sum_{k}\frac{w(w+1)\ldots(w+k-1)}{k(k-1)\ldots 1}z^{k}=\sum_{n,k}{k\brack n}z^{k}w^{n}/k!$.
(Alternatively, write it as $e^{w\ln(1/(1-z))}$ and expand first by powers of w.)
18. (a) For fixed n and varying r, the generating function is
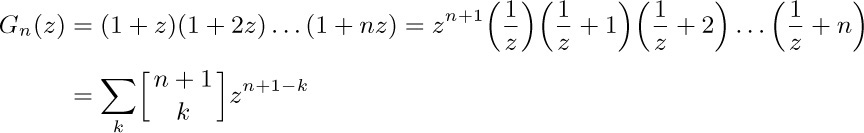
by Eq. (27). Hence the answer is ${n+1}\brack{n+1-r}$.
(b) Similarly, the generating function is
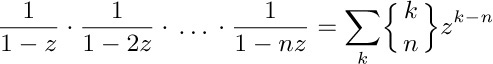
by Eq. (28), so the answer is ${n+r}\brace{n}$.
19. $\sum_{n\ge1}(1/n-1/(n+p/q))x^{p+nq}=$ $\sum_{k=0}^{q-1}\omega^{-kp}\ln(1-\omega^{k}x)-x^{p}\ln(1-x^{q})+\frac{q}{p}x^{p}=$ $f(x)+g(x)$, where $\omega=e^{2πi/q}$ and
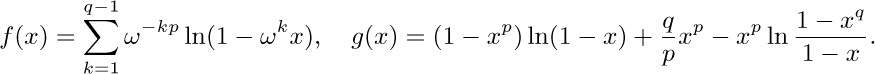
Now $\lim_{x→1-}g(x)=q/p-\ln q$. From the identity
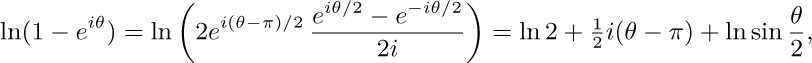
we may write $\lim_{x→1-}f(x)=f(1)=A+B$ where
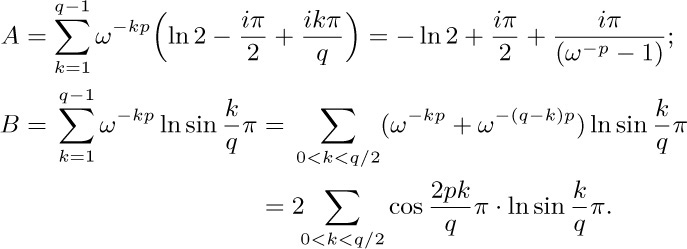
Finally,
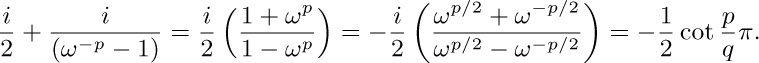
[Gauss derived these results in §33 of his monograph on hypergeometric series, Eq. [75], but with insufficient proof; Abel provided a justification in Crelle 1 (1826), 314–315.]
20. $c_{mk}=k!{m\brace k}$, by Eq. (1.2.6–(45).
21. We find $z^{2}G'(z)+zG(z)=G(z)-1$. The solution to this differential equation is $G(z)=(-1/z) e^{-1/z}(E_{1}(-1/z)+C)$, where $E_{1}(z)=\int_{z}^{\infty}e^{-t}\,dt/t$ and C is a constant. This function is very ill-behaved in the neighborhood of $z=0$, and $G(z)$ has no power series expansion. Indeed, since $\sqrt[n]{n!}\approx n/e$ is not bounded, the generating function does not converge in this case; it is, however, an asymptotic expansion for the stated function, when $z\lt 0$. [See K. Knopp, Infinite Sequences and Series (Dover, 1956), Section 66.]
22. $G(z)=(1+z)^{r}(1+z^{2})^{r}(1+z^{4})^{r}(1+z^{8})^{r}\ldots=(1-z)^{-r}$. It follows that the stated sum is $\mybinomf{r+n-1}{n}$.
23. (a) When $m=1$ this is the binomial theorem, with $f_{1}(z)=z$ and $g_{1}(z)=1+z$. When $m≥1$ we can increase m by 1 if we replace $z_{m}$ by $z_{m}(1+z_{m+1}^{-1})$ and let $f_{m+1}(z_{1},\ldots,z_{m+1})=$ $z_{m+1}f_{m}(z_{1},\ldots,z_{m-1},z_{m}(1+z_{m+1}^{-1}))$, $g_{m+1}(z_{1},\ldots,z_{m+1})=$ $z_{m+1}g_{m}(z_{1},\ldots,z_{m-1},z_{m}(1+z_{m+1}^{-1}))$. Thus $g_{2}(z_{1},z_{2})=z_{1}+z_{2}+z_{1}z_{2}$ and
Both polynomials $f_{m}$ and $g_{m}$ satisfy the same recurrence $f_{m}=z_{m}f_{m-1}+z_{m-1}f_{m-2}$, $g_{m}=z_{m}g_{m-1}+z_{m-1}g_{m-2}$, with the initial conditions $f_{-1}=0,f_{0}=g_{-1}=$ $g_{0}=z_{0}=1$. It follows that $g_{m}$ is the sum of all terms obtainable by starting with $z_{1}\ldots z_{m}$ and striking out zero or more nonadjacent factors; there are $F_{m+2}$ ways to do this. A similar interpretation applies to $f_{m}$, except that $z_{1}$ must remain. In part (b) we will encounter the polynomial $h_{m}=z_{m}g_{m-1}+z_{m-1}f_{m-2}$; this is the sum of all terms obtained from $z_{1}\ldots z_{m}$ by striking out factors that are not cyclically adjacent. For example, $h_{3}=z_{1}z_{2}z_{3}+z_{1}z_{2}+z_{1}z_{3}+z_{2}z_{3}$.
(b) By part (a), $S_{n}(z_{1},\ldots,z_{m-1},z)=[z_{m}^{n}]\sum_{r=0}^{n}z^{r}z_{m}^{n-r}f_{m}^{n-r}g_{m}^{r}$; hence
where $a=z_{m}g_{m-1}$, $b=z_{m-1}g_{m-2}$, $c=z_{m}f_{m-1}$, $d=z_{m-1}f_{m-2}$. Multiplying this equation by $z^{n}$ and summing first on n, then on r, then on s, yields the closed form
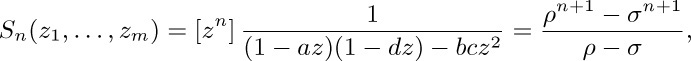
where $1-(a+d)z+(ad-bc)z^{2}=(1-ρz)(1-σz)$. Here $a+d=h_{m}$, and $ad-bc$ simplifies to $(-1)^{m}z_{1}\ldots z_{m}$. [We have, incidentally, established the recurrence $S_{n}=h_{m}S_{n-1}-(-1)^{m}z_{1}\ldots z_{m}S_{n-2}$, a relation that is not easy to derive without the help of generating functions.]
(c) Let $ρ_{1}=(z+\sqrt{z^{2}+4z})/2$ and $σ_{1}=(z-\sqrt{z^{2}+4z})/2$ be the roots when $m=1$; then $ρ_{m}=ρ_{1}^{m}$ and $σ_{m}=σ_{1}^{m}$.
Carlitz used this result to deduce a surprising fact: The characteristic polynomial $\det(xI-A)$ of the $n×n$ matrix
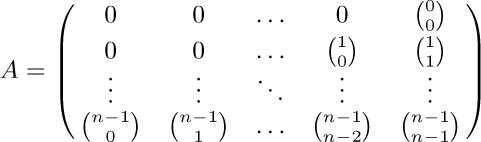
of “right justified binomial coefficients” is $\sum_{k}\mybinomf{n}{k}_{\!\cal F}(-1)^{\lceil{(n-k)/2}\rceil}x^{k}$, with Fibonomial coefficients (see exercise 1.2.8–30). He also showed, using similar methods, that

[Collectanea Math. 27 (1965), 281–296.]
24. Both sides are equal to $\sum_{k}\mybinomf{m}{k}[z^{n}](zG(z))^{k}$. When $G(z)=1/(1-z)$, the identity becomes $\sum_{k}\mybinomf{m}{k}\mybinomf{n-1}{n-k}=\mybinomf{m+n-1}{n}$, a case of 1.2.6–(21). When $G(z)=(e^{z}-1)/z$, it becomes $\sum_{k}m^{\underline k}{n\brace k}=m^{n}$, Eq. 1.2.6–(45).
25. $Σ_{k}[w^{k}](1-2w)^{n}[z^{n}]z^{k}(1+z)^{2n-2k}=$ $[z^{n}](1+z)^{2n}Σ_{k}[w^{k}](1-2w)^{n}(z/(1+z)^{2})^{k}$, which equals $[z^{n}](1+z)^{2n}(1-2z/(1+z)^{2})^{n}=$ $[z^{n}](1+z^{2})^{n}=\mybinomf{n}{n/2}[n\rm\;even]$. Similarly, we find $\sum_{k}\mybinomf{n}{k}\mybinomf{2n-2k}{n-k}(-4)^{k}=(-1)^{n}\mybinomf{2n}{n}$. Many examples of this summation technique can be found in G. P. Egorychev’s book Integral Representation and the Computation of Combinatorial Sums (Amer. Math. Soc., 1984), translated from the Russian edition of 1977.
26. $[F(z)]G(z)$ denotes the constant term of $F(z^{-1})G(z)$. See the discussion by D. E. Knuth in A Classical Mind (Prentice–Hall, 1994), 247–258.
1. $G_{n}(0)=1/n$; this is the probability that $X[n]$ is the largest.
2. $G''(1)=Σ_{k}k(k-1)p_{k}$, $G'(1)=Σ_{k}kp_{k}$.
3. (min 0, ave 6.49, max 999, dev 2.42). Note that $H_{n}^{(2)}$ is approximately $π^{2}/6$; see Eq. 1.2.7–(7).
4. $\mybinomf{n}{k}p^{k}q^{n-k}$.
5. The mean is $36/5=7.2$; the standard deviation is $6\sqrt{2}/5\approx1.697$.
$\ln(q+pe^{t})=\ln\left(1+pt+\frac{pt^{2}}{2}+\frac{pt^{3}}{6}+\cdots\right)=pt+p(1-p)\frac{t^{2}}{2}+p(1-p)(1-2p)\frac{t^{3}}{6}+\cdots$
tells us that $κ_{3}/n=p(1-p)(1-2p)=pq(q-p)$. (This nice pattern does not continue to the coefficient of $t^{4}$.) Setting $p=k^{-1}$ gives us $κ_3=\sum_{k=2}^{n}k^{-1}(1-k^{-1})(1-2k^{-1})=H_{n}-3H_{n}^{(2)}+2H_{n}^{(3)}$ in the case of distribution (8). And for (20), we have $\ln G(e^{t})=t+H(nt)-H(t)$ where $H(t)=\ln((e^{t}-1)/t)$. Since $H'(t)=e^{t}/(e^{t}-1)-1/t$, we have $κ_{r}=(n^{r}-1) B_{r}/r$ for all r ≥ 2 in this case; in particular, $κ_{3}=0$.
7. The probability that A = k is $p_{mk}$. For we may consider the values to be $1,2,\ldots,m$. Given any partitioning of the n positions into m disjoint sets, there are $m!$ ways to assign the numbers $1,\ldots,m$ to these sets. Algorithm M treats these values as if only the rightmost element of each set were present; so $p_{mk}$ is the average for any fixed partitioning. For example, if n = 5, m = 3, one partition is
$\{X[1],X[4]\}$ $\{X[2],X[5]\}$ $\{X[3]\}$;
the arrangements possible are 12312, 13213, 21321, 23123, 31231, 32132. In every partition we get the same percentage of arrangements with A = k.
On the other hand, the probability distribution does change if more information is given. If n = 3 and m = 2, for example, our argument in the previous paragraph considers the six possibilities 122, 212, 221, 211, 121, 112; if we know that there are two 2s and one 1, then only the first three of these possibilities should be considered. But this interpretation is not consistent with the statement of the exercise.
8. $M^{\underline n}/M^{n}$. The larger M is, the closer this probability gets to one.
9. Let $q_{nm}$ be the probability that exactly m distinct values occur; then from the recurrence
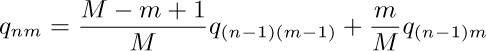
we deduce that
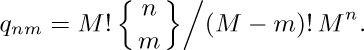
See also exercise 1.2.6–64.
10. This is $q_{nm}p_{mk}$ summed over all m, namely $M^{-n}\sum_{m}\mybinomf{M}{m}{n\brace m}{m\brack k+1}$. There does not appear to be a simple formula for the average, which is one less than
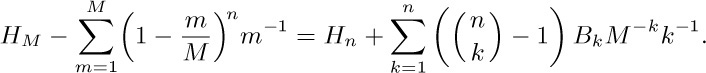
11. Since this is a product, we add the semi-invariants of each term. If $H (z)=z^{n}$, $H (e^{t})=e^{nt}$, so we find $κ_{1}=n$ and all others are zero. Therefore, mean(F) = n + mean(G), and all other semi-invariants are unchanged. (This accounts for the name “semi-invariant.”)
12. The first identity is obvious by writing out the power series for $e^{kt}$. For the second, let $u=1+M_{1}t+M_{2}t^{2}/2!+\cdots$; when t = 0 we have u = 1 and $D_{t}^{k}u=M_{k}$. Also, $D_{u}^{j}(\ln u)=(-1)^{j-1}(j-1)!/u^{j}$. By exercise 11, the same formula applies for central moments except that we leave out all terms with $k_{1}\gt 0$; thus $κ_{2}=m_{2}$, $κ_{3}=m_{3}$, $κ_{4}=m_{4}-3m_{2}^{2}$.
13. $\displaystyle G_{n}(z)=\frac{\varGamma(n+z)}{\varGamma(z+1)n!}=\frac{e^{-z}(n+z)^{z-1}}{\varGamma(z+1)}\left(1+\frac{z}{n}\right)^{n}(1+O(n^{-1}))=\frac{n^{z-1}}{\varGamma(z+1)}(1+O(n^{-1}))$. Let $z_{n}=e^{it/σ_{n}}$. When $n→∞$ and t is fixed, we have $z_{n}→1$; hence $\varGamma(z_{n}+1)→1$, and
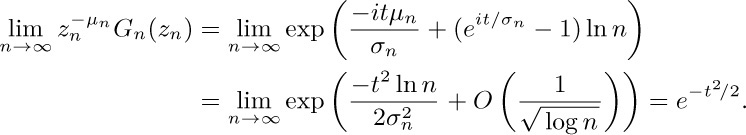
Notes: This is a theorem of Goncharov [Izv. Akad. Nauk SSSR Ser. Math. 8 (1944), 3–48]. P. Flajolet and M. Soria [Disc. Math. 114 (1993), 159–180] have extended the analysis to show that $G_{n}(z)$ and a large family of related distributions not only are approximately normal near their mean values, they also have uniformly exponential tails, in the sense that
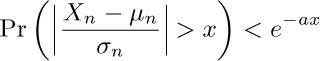
for some positive constant a and for all n and x.
14. $e^{-itpn/\sqrt{pqn}}(q+pe^{it/\sqrt{pqn}})^{n}=(qe^{-itp/\sqrt{pqn}}+pe^{itq/\sqrt{pqn}})^{n}$. Expand the exponentials in power series, to get $(1-t^{2}/2n+O(n^{-3/2}))^{n}=\exp(n\ln(1-t^{2}/2n+O(n^{-3/2})))=\exp(-t^{2}/2+O(n^{-1/2}))→\exp(-t^{2}/2)$.
15. (a)$\sum_{k\ge0}e^{-μ}(μz)^{k}/k!=e^{μ(z-1)}$. (b) $\ln e^{μ(e^{t}-1)}=μ(e^{t}-1)$, so all semi-invariants equal μ. (c) $\exp(-itnp/\sqrt{np})\exp(np(it/\sqrt{np}-t^{2}/(2np)+O(n^{-3/2})))=$ $\exp(-t^{2}/2+O(n^{-1/2}))$.
16. $g(z)=∑_{k}p_{k}g_{k}(z)$; ${\rm mean}(g)=∑_{k}p_{k}\,{\rm mean}(g_{k})$; and ${\rm var}(g)=∑_{k}p_{k}\,{\rm var}(g_{k})+∑_{j\lt k}p_{j}p_{k}({\rm mean}(g_{j})-{\rm mean}(g_{k}))^{2}$.
17. (a) The coefficients of $f(z)$ and $g(z)$ are nonnegative, and $f(1)=g(1)=1$. Clearly $h(z)$ shares these same characteristics, since $h(1)=g(f(1))$, and the coefficients of h are polynomials in those of $f$ and g, with nonnegative coefficients.
(b) Let $f(z)=∑p_{k}z^{k}$ where $p_{k}$ is the probability that some event yields a “score” of k. Let $g(z)=∑q_{k}z^{k}$ where $q_{k}$ is the probability that the event described by $f$ happens exactly k times (each occurrence of the event being independent of the others). Then $h(z)=∑r_{k}z^{k}$, where $r_{k}$ is the probability that the sum of the scores of the events that occurred is equal to k. (This is easy to see if we observe that $f(z)^{k}=∑s_{t}z^{t}$, where $s_{t}$ is the probability that a total score t is obtained in k independent occurrences of the event.) Example: If $f$ gives the probabilities that a woman has k female offspring, and if g gives the probabilities that there are k females in the nth generation, then h gives the probabilities that there are k females in the (n + 1)st generation, assuming independence.
(c) ${\rm mean}(h)={\rm mean}(g)\,{\rm mean}(f)$; ${\rm var}(h)={\rm var}(g)\,{\rm mean}^{2}(f)+{\rm mean}(g)\,{\rm var}(f)$.
18. Consider the choice of $X[1],\ldots,X[n]$ as a process in which we first place all the n’s, then place all the (n − 1)’s among these $n\unicode{39}\rm s,\ldots,$ finally place the ones among the rest. As we place the r’s among the numbers $\{r+1,\ldots,n\}$, the number of local maxima from right to left increases by one if and only if we put an r at the extreme right. This happens with probability $k_{r}/(k_{r}+k_{r+1}+\cdots+k_{n})$.
19. Let $a_{k}=l$. Then $a_{k}$ is a left-to-right maximum of $a_{1}\ldots a_{n}⇔j\lt k$ implies $a_{j}\lt l⇔a_{j}\gt l$ implies $j\gt k⇔j\gt l$ implies $b_{j}\gt k⇔k$ is a right-to-left minimum of $b_{1}\ldots b_{n}$.
20. We have $m_{L}=\max\{a_{1}-b_{1},\ldots,a_{n}-b_{n}\}$. Proof: If not, let k be the smallest subscript such that $a_{k}-b_{k}\gt m_{L}$. Then $a_{k}$ is not a left-to-right maximum, so there is a j < k with $a_{j}≥a_{k}$. But then $a_{j}-b_{j}≥a_{k}-b_{k}\gt m_{L}$, contradicting the minimality of k. Similarly, $m_{R}=\max\{b_{1}-a_{1},\ldots,b_{n}-a_{n}\}$.
21. The result is trivial when $\epsilon≥q$, so we may assume that $\epsilon\lt q$. Setting $x=\frac{p+\epsilon}{p}\frac{q}{q-\epsilon}$ in (25) gives $\Pr(X\ge n(p+\epsilon))\le((\frac{p}{p+\epsilon})^{p+\epsilon}(\frac{q}{q-\epsilon})^{q-\epsilon})^{n}$. Now $(\frac{p}{p+\epsilon})^{p+\epsilon}\le e^{-\epsilon}$ since $t≤e^{t-1}$ for all real t. And $(q-\epsilon)\ln\frac{q}{q-\epsilon}=\epsilon-\frac{1}{2\cdot1}\epsilon^{2}q^{-1}-\frac{1}{3\cdot2}\epsilon^{3}q^{-2}-\cdots≤\epsilon-\frac{1}{2q}\epsilon^{2}$. (A more detailed analysis yields the slightly stronger estimate $\exp(-\epsilon^{2}n/(2pq))$ when $p\ge\frac12$; still further work yields the upper bound $\exp(-2\epsilon^{2}n)$ for all p.)
By reversing the roles of heads and tails we find
$\Pr(X≤n(p-\epsilon))=\Pr(n-X≥n(q+\epsilon))≤e^{-\epsilon^{2}n/(2p)}$.
(One should not confuse “tails” with the tail of a probability distribution.)
22. (a) Set x = r in (24) and (25), and note that $q_{k}+p_{k}r=1+(r-1)p_{k}≤e^{(r-1)p_{k}}$. [See H. Chernoff, Annals of Math. Stat. 23 (1952), 493–507.]
(b) Let $r=1+δ$ where $|δ|≤1$. Then $r^{-r}e^{r-1}=\exp(-\frac{1}{2\cdot1}\delta^{2}+\frac{1}{3\cdot2}\delta^{3}-\cdots)$, which is $≤e^{-δ^{2}/2}$ when δ ≤ 0 and $≤e^{-δ^{2}/3}$ when δ ≥ 0.
(c) The function $r^{-1}e^{1-1/r}$ decreases from 1 to 0 as r increases from 1 to ∞. If r ≥ 2 it is $≤e^{1/2}/2\lt .825$; if $r≥4.32$ it is $\lt 1/2$.
Incidentally, the tail inequalities with x = r give precisely the same estimate $(r^{-r}e^{r-1})^{μ}$ when X has the Poisson distribution of exercise 15.
23. Setting $x=\frac{p-\epsilon}{p}\frac{q}{q-\epsilon}$ in (24) gives $\Pr(X≤n(p-\epsilon))≤((\frac{p}{p-\epsilon})^{p-\epsilon}(\frac{q-\epsilon}{q})^{q-\epsilon})^{n}≤e^{-\epsilon^{2}n/(2pq)}$. Similarly, $x=\frac{p+\epsilon}{p}\frac{q}{q+\epsilon}$ yields $\Pr(X\ge n(p+\epsilon))≤((\frac{p}{p+\epsilon})^{p+\epsilon}(\frac{q+\epsilon}{q})^{q+\epsilon})^{n}$. Let $f(\epsilon)=(q+\epsilon)\ln(1+\frac{\epsilon}{q})-(p+\epsilon)\ln(1+\frac{\epsilon}{p})$, and note that $f'(\epsilon)=\ln(1+\frac{\epsilon}{q})-\ln(1+\frac{\epsilon}{p})$. It follows that $f(\epsilon)≤-\epsilon^{2}/(6pq)$ if $0≤\epsilon≤p$.
1. Zero.
2. Each O-symbol represents a different approximate quantity; since the left-hand side might be $f(n)-(-f(n))=2f(n)$, the best we can say is $O(f(n))-O(f(n))=O(f(n))$, which follows from (6) and (7). To prove (7), note that if $|x_{n}|≤M|f(n)|$ for $n≥n_{0}$ and $|x'_n|≤M'|f(n)|$ for $n≥n'_{0}$, then $|x_{n}\pm x'_n|≤|x_n|+|x'_n|≤(M+M')|f(n)|$ for $n≥\max(n_{0},n'_{0})$. (Signed, J. H. Quick, student.)
3. $n(\ln n)+\gamma n+O(\sqrt{n}\ln n)$.
4. $\ln a+(\ln a)^{2}/2n+(\ln a)^{3}/6n^{2}+O(n^{-3})$.
5. If $f(n)=n^{2}$ and $g(n)=1$, then n belongs to the set $O(f(n)+g(n))$ but not to the set $f(n)+O(g(n))$. So the statement is false.
6. A variable number, n, of O-symbols has been replaced by a single O-symbol, falsely implying that a single value of M will suffice for each term $|kn|≤Mn$. The given sum is actually $Θ(n^{3})$, as we know. The last equality, $\sum_{k=1}^{n}O(n)=O(n^{2})$, is perfectly valid.
7. If x is positive, the power series 1.2.9–(22) tells us that $e^{x}\gt x^{m+1}/(m+1)!$; hence the ratio of $e^{x}/x^{m}$ is unbounded by any M.
8. Replace n by $e^{n}$ and apply the method of the previous exercise.
9. If $|f(z)|≤M|z|^{m}$ for $|z|≤r$, then $|e^{f(z)}|≤e^{M|z|^{m}}=1+|z|^{m}(M+M^{2}|z|^{m}/2!+$ $M^{3}|z|^{2m}/3!+\cdots)≤$ $1+|z|^{m}(M+M^{2}r^{m}/2!+M^{3}r^{2m}/3!+\cdots)$.
10. $\ln(1+O(z^{m}))=O(z^{m})$, if m is a positive integer. Proof: If $f(z)=O(z^{m})$, there exist positive numbers r < 1, r′ < 1, and a constant M such that $|f(z)|≤M|z|^{m}≤r'$ when $|z|≤r$. Then $|\ln(1+f(z))|\le|f(z)|+$ $\frac12|f(z)|^{2}+\cdots\le|z|^{m}M(1+\frac{1}{2}r'+\cdots)$.
11. We can apply Eq. (12) with m = 1 and $z=\ln n/n$. This is justified since $\ln n/n≤r$ for any given r > 0, when n is sufficiently large.
12. Let $f(z)=(ze^{z}/(e^{z}-1))^{1/2}$. If ${1/2}\brack{1/2-k}$ were $O(n^{k})$, the stated identity would show that $[z^{k}]f(z)=O(n^{k}/(k-1)!)$, so $f(z)$ would converge when $z=2πi$. But $f(2πi)=∞$.
13. Proof: We may take $L=1/M$ in the definitions of O and Ω.
1. $(B_{0}+B_{1}z+B_{2}z^{2}/2!+\cdots) e^{z}=(B_{0}+B_{1}z+B_{2}z^{2}/2!+\cdots)+z$; apply Eq. 1.2.9–(11).
2. The function $B_{m+1}(\{x\})$ must be continuous, for the integration by parts.
3. $|R_{mn}|\le|B_m/(m)!|\int_{1}^{n}|f^{(m)}(x)|\,dx$. [Notes: We have $B_{m}(x)=(-1)^{m}B_{m}(1-x)$, and $B_{m}(x)$ is $m!$ times the coefficient of $z^{m}$ in $ze^{xz}/(e^{z}-1)$. In particular, since $e^{z/2}/(e^{z}-1)=1/(e^{z/2}-1)-1/(e^{z}-1)$ we have $B_{m}(\frac12)=(2^{1-m}-1)B_{m}$. It is not difficult to prove that the maximum of $|B_{m}-B_{m}(x)|$ for $0≤x≤1$ occurs at $x=\frac{1}{2}$ when m is even. Now when $m=2k≥4$, let us write simply $R_{m}$ and $C_{m}$ for the quantities $R_{mn}$ and $C_{mn}$. We have $R_{m-2}=C_{m}+R_{m}=\int_{1}^{n}(B_{m}-B_{m}(\{x\}))f^{(m)}(x)\,dx/m!$, and $B_{m}-B_{m}(\{x\})$ is between 0 and $(2-2^{1-m})B_{m}$; hence $R_{m-2}$ lies between 0 and $(2-2^{1-m})C_{m}$. It follows that $R_{m}$ lies between $-C_{m}$ and $(1-2^{1-m})C_{m}$, a slightly stronger result. According to this argument we see that if $f^{(m+2)}(x)f^{(m+4)}(x)\gt 0$ for $1\lt x\lt n$, the quantities $C_{m+2}$ and $C_{m+4}$ have opposite signs, while $R_{m}$ has the sign of $C_{m+2}$ and $R_{m+2}$ has the sign of $C_{m+4}$ and $|R_{m+2}|≤|C_{m+2}|$; this proves (13). See J. F. Steffensen, Interpolation (Baltimore: 1927),§14.]
4. $\displaystyle\sum_{0\le k\lt n}k^{m}=\frac{n^{m+1}}{1+m}+\sum_{k=1}^{m}\frac{B_k}{k!}\frac{m!}{(m-k+1)!}n^{m-k+1}=$ $\displaystyle\frac{1}{m+1}B_{m+1}(n)-\frac{1}{m+1}B_{m+1}$.
5. It follows that
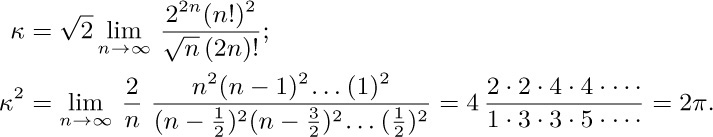
6. Assume that $c\gt 0$ and consider $∑_{0≤k\lt n}\ln(k+c)$. We find
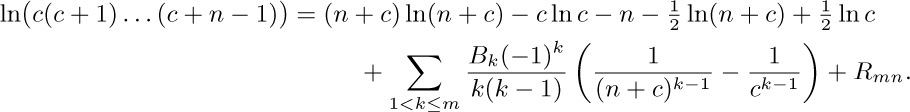
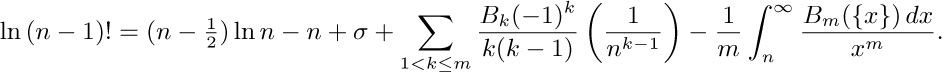
Now $\ln \varGamma_{n-1}(c)=c\ln(n-1)+\ln(n-1)!-\ln(c\ldots(c+n-1))$; substituting and letting $n→∞$, we get
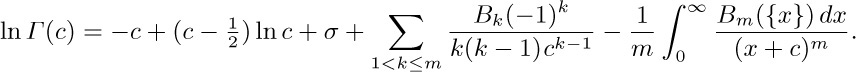
This shows that $\varGamma(c+1)=ce^{\ln \varGamma(c)}$ has the same expansion we derived for c!.
7. $A\,n^{n^{2}/2+n/2+1/12}e^{-n^{2}/4}$ where A is a constant. To obtain this result, apply Euler’s summation formula to $\sum_{k=1}^{n-1}k\ln k$. A more accurate formula is obtained if we multiply the answer above by
$\exp(-B_{4}/(2·3·4n^{2})-\cdots-B_{2t}/((2t-2)(2t-1)(2t)n^{2t-2})+O(1/n^{2t}))$.
In these formulas, A is the “Kinkelin–Glaisher constant” 1.2824271… [Crelle 57 (1860), 122–158; Messenger of Math. 7 (1877), 43–47], which can be shown to equal $e^{1/12-\zeta'(-1)}=(2πe^{γ-\zeta'(2)/\zeta(2)})^{1/12}$ [de Bruijn, Asymptotic Methods in Analysis,§3.7].
8. We have, for example, $\ln(an^{2}+bn)=2\ln n+\ln a+\ln(1+b/(an))$. Thus the answer to the first question is found to be $2an^{2}\ln n+a(\ln a-1)n^{2}+2bn\ln n+bn\ln a+\ln n+b^{2}/(2a)+\frac12\ln a+σ+(3a-b^{2})b/(6a^{2}n)+O(n^{-2})$. Massive cancellation occurs when we compute the quantity $\ln(cn^{2})!-\ln (cn^{2}-n)!-n\ln c-\ln n^{2}!+\ln(n^{2}-n)!=$ $(c-1)/(2c)-(c-1)(2c-1)/(6c^{2}n)+O(n^{-2})$. The answer is therefore
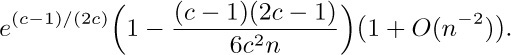
Incidentally, $\mybinomf{cn^{2}}{n}/{\big(}c^{n}\mybinomf{n^{2}}{n}{\big)}$ can be written $\prod_{j=1}^{n-1}(1+\alpha j/(n^{2}-j))$ where $α=1-1/c$.
9. (a) We have $\ln(2n)!=(2n+\frac12)\ln 2n-2n+\sigma+\frac{1}{24n}+O(n^{-3})$, and $\ln(n!)^{2}=(2n+1)\ln n-2n+2\sigma+\frac{1}{6n}+O(n^{-3})$; hence $\mybinomf{2n}{n}=\exp(2n\ln 2-\frac12\ln\pi n-\frac{1}{8n}+O(n^{-3}))=$ $2^{2n}(\pi n)^{-1/2}(1-\frac{1}{8}n^{-1}+\frac{1}{128}n^{-2}+O(n^{-3}))$. (b) Since $\mybinomf{2n}{n}=2^{2n}\mybinomf{n-1/2}{n}$ and $\mybinomf{n-1/2}{n}=\varGamma(n+1/2)/(n\varGamma(n)\varGamma(1/2))=$ $n^{-1}n^{\overline{1/2}}/\sqrt{\pi}$, we obtain the same result from 1.2.11.1–(16) because
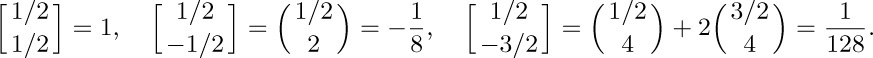
Method (b) explains why the denominators in
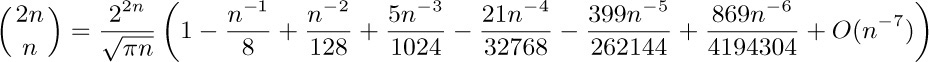
are all powers of 2 [Knuth and Vardi, AMM 97 (1990), 629–630].
1. Integrate by parts.
2. Substitute the series for $e^{-t}$ in the integral.
3. See Eq. exercise 1.2.6–48.
4. $1+1/u$ is bounded as a function of v, since it goes to zero as v goes from r to infinity. Replace it by M and the resulting integral is $Me^{-rx}$.
5. $f''(x)=f(x)((n+1/2)(n-1/2)/x^{2}-(2n+1)/x+1)$ changes sign at the point $r=n+1/2-\sqrt{n+1/2}$, so $|R|=O(\int_{0}^{n}|f''(x)|\,dx)=$ $O(\int_{0}^{r}f''(x)\,dx-\int_{r}^{n}f''(x)\,dx)=$ $O(f'(n)-2f'(r)+f'(0))=$ $O(f(n)/\sqrt{n})$.
6. It is $n^{n+β}\exp((n+β)(α/n-α^{2}/2n^{2}+O(n^{-3})))$, etc.
7. The integrand as a power series in $x^{-1}$ has the coefficient of $x^{-n}$ as $O(u^{2n})$. After integration, terms in $x^{-3}$ are $Cu^{7}/x^{3}=O(x^{-5/4})$, etc. To get $O(x^{-2})$ in the answer, we can discard terms $u^{n}/x^{m}$ with $4m-n≥9$. Thus, an expansion of the product $\exp(-u^{2}/2x)\exp(u^{3}/3x^{2})\ldots$ leads ultimately to the answer
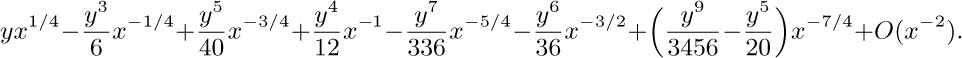
8. (Solution by Miklós Simonovits.) We have $|f(x)|\lt x$ if x is large enough. Let $R(x)=\int_{0}^{f(x)}(e^{-g(u,x)}-e^{-h(u,x)})du$ be the difference between the two given integrals, where $g(u,x)=u-x\ln(1+u/x)$ and $h(u,x)=u^{2}/2x-u^{3}/3x^{2}+\cdots+(-1)^{m}u^{m}/mx^{m-1}$. Notice that $g(u,x)≥0$ and $h(u,x)≥0$ when $|u|\lt x$; also $g(u,x)=h(u,x)+O(u^{m+1}/x^{m})$.
According to the mean value theorem, $e^{a}-e^{b}=(a-b) e^{c}$ for some c between a and b. Therefore $|e^{a}-e^{b}|≤|a-b|$ when a, b ≤ 0. It follows that
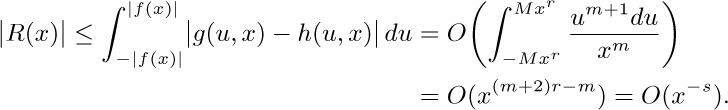
9. We may assume that p ≠ 1, since p = 1 is given by Theorem A. We also assume that p ≠ 0, since the case p = 0 is trivial.
Case 1: p < 1. Substitute $t=px(1-u)$ and then $v=-\ln(1-u)-pu$. We have $dv=((1-p+pu)/(1-u))du$, so the transformation is monotone for 0 ≤ u ≤ 1, and we obtain an integral of the form
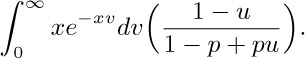
Since the parenthesized quantity is $(1-p)^{-1}(1-v(1-p)^{-2}+\cdots)$, the answer is
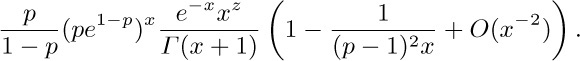
Case 2: p > 1. This is $1-\int_{px}^{\infty}(\;)$. In the latter integral, substitute $t=px(1+u)$, then $v=pu-\ln(1+u)$, and proceed as in Case 1. The answer turns out to be the same formula as Case 1, plus one. Notice that $pe^{1-p}\lt 1$, so $(pe^{1-p})^{x}$ is very small.
The answer to exercise 11 gives another way to solve this problem.
10. $\frac{p}{p-1}(pe^{1-p})^{x}e^{-x}x^{x}\left(1-e^{-y}-\frac{e^{-y}(e^{y}-1-y-y^{2}/2)}{x(p-1)^{2}}+O(x^{-2})\right)$.
11. First, $xQ_{x}(n)+R_{1/x}(n)=n!\,(x/n)^{n}e^{n/x}$ generalizes (4). Next, we have $R_{x}(n)=n!\,(e^{x}/nx)^{n}γ(n,nx)/(n-1)!$, generalizing (9). Since $aγ(a,x)=γ(a+1,x)+e^{-x}x^{a}$ we can also write $R_{x}(n)=1+(e^{x}/nx)^{n}γ(n+1,nx)$, relating this problem to exercise 9.
Moreover, we can tackle $Q_{x}(n)$ and $R_{x}(n)$ directly by using Eqs. 1.2.9–(27) and (28) to derive series expansions involving Stirling numbers:
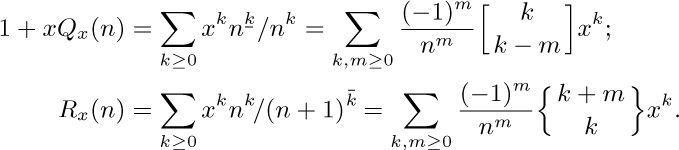
The sums over k are convergent for fixed m when $|x|\lt 1$, and when $|x|\gt 1$ we can use the relation between $Q_{x}(n)$ and $R_{1/x}(n)$; this leads to the formulas
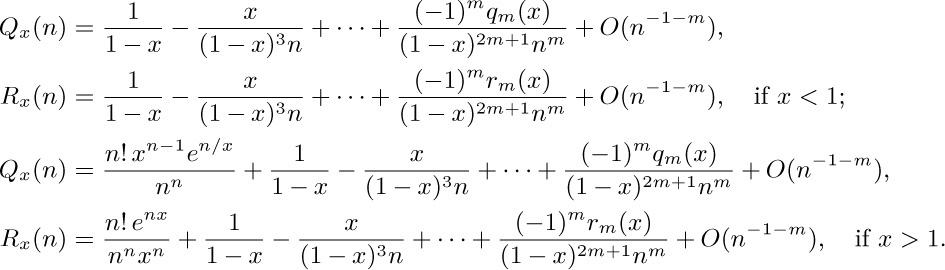
Here
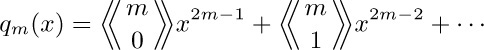
and
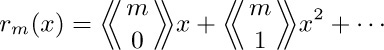
are polynomials whose coefficients are “second-order Eulerian numbers” [CMath §6.2; see L. Carlitz, Proc. Amer. Math. Soc. 16 (1965), 248–252]. The case $x=-1$ is somewhat delicate, but it can be handled by continuity, because the bound implied by $O(n^{-1-m})$ is independent of x when $x\lt 0$. It is interesting to note that $R_{-1}(n)-Q_{-1}(n)=(-1)^{n}n!/(e^{n}n^{n})\approx(-1)^{n}\sqrt{2\pi n}/e^{2n}$ is extremely small.
12. $γ(\frac{1}{2},\frac{1}{2}x^{2})/\sqrt{2}$.
13. See P. Flajolet, P. Grabner, P. Kirschenhofer, and H. Prodinger, J. Computational and Applied Math. 58 (1995), 103–116.
15. Expanding the integrand by the binomial theorem, we obtain $1+Q(n)$.
16. Write $Q(k)$ as a sum, and interchange the order of summation using Eq. 1.2.6–(53).
17. $S(n)=\sqrt{\pi n/2}+\frac{2}{3}-\frac{1}{24}\sqrt{\pi/2n}-$ $\frac{4}{135}n^{-1}+\frac{49}{1152}\sqrt{\pi/2n^{3}}+O(n^{-2})$. [Note that $S(n+1)+P(n)=∑_{k≥0}k^{n-k}k!/n!$, while $Q(n)+R(n)=∑_{k≥0}n!/k!\,n^{n-k}$.]
18. Let $S_{n}(x,y)=∑_{k}\mybinomf{n}{k}(x+k)^{k}(y+n-k)^{n-k}$. Then for $n\gt 0$ we have $S_{n}(x,y)=x∑_{k}\mybinomf{n}{k}(x+k)^{k-1}(y+n-k)^{n-k}+$ $n∑_{k}\mybinomf{n-1}{k}(x+1+k)^{k}(y+n-1-k)^{n-1-k}=$ $(x+y+n)^{n}+nS_{n-1}(x+1,y)$ by Abel’s formula 1.2.6–(16); consequently $S_{n}(x,y)=∑_{k}\mybinomf{n}{k}k!\,(x+y+n)^{n-k}$. [This formula is due to Cauchy, who proved it using the calculus of residues; see his Œuvres (2) 6, 62–73.] The stated sums are therefore equal respectively to $n^{n}(1+Q(n))$ and $(n+1)^{n}Q(n+1)$.
19. Suppose $C_{n}$ exists for all $n≥N$ and $|f(x)|≤Mx^{α}$ for $0≤x≤r$. Let $F(x)=\int_{r}^{x}e^{-Nt}f(t)\,dt$. Then when $n\gt N$ we have
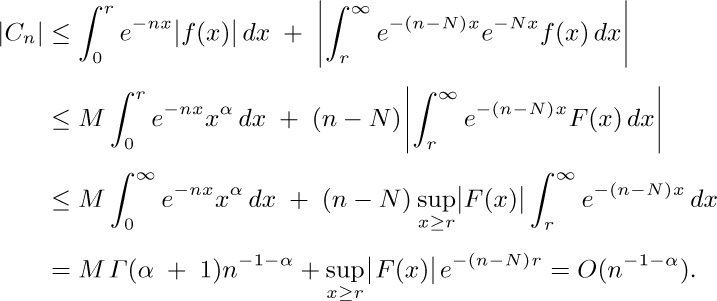
[E. W. Barnes, Phil. Trans. A206 (1906), 249–297; G. N. Watson, Proc. London Math. Soc. 17 (1918), 116–148.]
20. [C. C. Rousseau, Applied Math. Letters 2 (1989), 159–161.] We have $Q(n)+1=n\int_{0}^{\infty}e^{-nx}(1+x)^{n}\,dx=$ $n\int_{0}^{\infty}e^{-n(x-\ln(1+x))}\,dx=n\int_{0}^{\infty}e^{-nu}g(u)\,du$, by substituting $u=x-\ln(1+x)$ and letting $g(u)=dx/du$. Notice that $x=\sum_{k=1}^{\infty}c_{k}(2u)^{k/2}$ when u is sufficiently small. Hence $g(u)=\sum_{k=1}^{m-1}kc_{k}(2u)^{k/2-1}+O(u^{m/2-1})$, and we can apply Watson’s lemma to $Q(n)+1-n\int_{0}^{\infty}e^{-nu}\sum_{k=1}^{m-1}kc_{k}(2u)^{k/2-1}\,du$.
1. Four; each byte would then contain $3^{4}=81$ different values.
2. Five, since five bytes is always adequate but four is not.
3. $(0{\colon}2)$; $(3{\colon}3)$; $(4{\colon}4)$; $(5{\colon}5)$.
4. Presumably index register 4 contains a value greater than or equal to 2000, so that a valid memory address results after indexing.
5. ‘DIV -80,3(0:5)’ or simply ‘DIV -80,3’.
6. (a)  .
.
(b) ${\rm rI2}←-200$.
(c)  .
.
(d) Undefined; we can’t load such a big value into an index register.
(e)  .
.
7. Let $n=\rm|rAX|$ be the magnitude of registers A and X before the operation, and let $d=\rm|V|$ be the magnitude of the divisor. After the operation the magnitude of rA is $\lfloor{n/d}\rfloor$, and the magnitude of rX is $n\bmod d$. The sign of rX afterwards is the previous sign of rA; the sign of rA afterwards is + if the previous signs of rA and V were the same, otherwise it is −.
Stating this another way: If the signs of rA and V are the same, $\rm rA←\lfloor{rAX/V}\rfloor$ and $\rm rX←rAX\bmod V$. Otherwise $\rm rA←\lceil{rAX/V}\rceil$ and $\rm rX←rAX\bmod-V$.
8.  ;
;  .
.
9. ADD, SUB, DIV, NUM, JOV, JNOV, INCA, DECA, INCX, DECX.
10. CMPA, CMP1, CMP2, CMP3, CMP4, CMP5, CMP6, CMPX. (Also FCMP, for floating point.)
11. MOVE, LD1, LD1N, INC1, DEC1, ENT1, ENN1.
12. INC3 0,3.
13. ‘JOV 1000’ makes no difference except time. ‘JNOV 1001’ makes a different setting of rJ in most cases. ‘JNOV 1000’ makes an extraordinary difference, since it may lock the computer in an infinite loop.
14. NOP with anything; ADD, SUB with $\rm F=(0{\colon}0)$ or with address equal to * (the location of the instruction) and $\rm F=(3{\colon}3)$; HLT (depending on how you interpret the statement of the exercise); any shift with address and index zero; SLC or SRC with index 0 and address a multiple of 10; MOVE with F = 0; STJ *(0:0), STZ *(0:0), and STZ *(3:3); JSJ *+1; any of the INC or DEC instructions with address and index zero. But ‘ENT1 0,1’ is not always a no-op, because it might change rI1 from −0 to +0.
15. 70; 80; 120. (The block size times 5.)
16. (a) STZ 0; ENT1 1; MOVE 0(49); MOVE 0(50). If the byte size were known to equal 100, only one MOVE instruction would have been necessary, but we are not allowed to make assumptions about the byte size.
(b) Use 100 STZ’s.
17. (a) STZ 0,2; DEC2 1; J2NN 3000.
(b) 
(A slightly faster, but quite preposterous, program uses 993 STZ’s: JMP 3995; STZ 1,2; STZ 2,2; …; STZ 993,2; J2N 3999; DEC2 993; J2NN 3001; ENN1 0,2; JMP 3000,1.)
18. (If you have correctly followed the instructions, an overflow will occur on the ADD, with minus zero in register A afterwards.) Answer: Overflow is set on, comparison is set EQUAL, rA is set to  , rX is set to
, rX is set to  , rI1 is set to +3, and memory locations 0001, 0002 are set to +0. (Unless the program itself begins in location 0000.)
, rI1 is set to +3, and memory locations 0001, 0002 are set to +0. (Unless the program itself begins in location 0000.)
19. $42u=(2+1+2+2+1+1+1+$ $2+2+1+2+2+3+10+10)u$.
20. 
21. (a) Not unless it can be set to zero by external means (see the “GO button”, exercise 26), since a program can set ${\rm rJ}←N$ only by jumping from location $N-1$.
(b) 
22. Minimum time: If b is the byte size, the assumption that $|X^{13}|\lt b^{5}$ implies that $X^{2}\lt b$, so $X^{2}$ can be contained in one byte. The following ingenious solution due to Y. N. Patt makes use of this fact. The sign of rA is the sign of X.
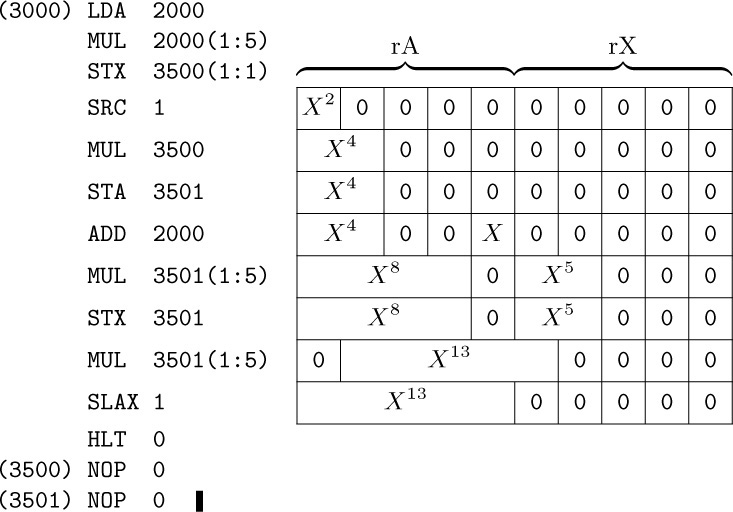
space = 14; time = 54u, not counting the HLT.
At least five multiplications are “necessary,” according to the theory developed in Section 4.6.3, yet this program uses only four! And in fact there is an even better solution below.

True minimum time: As R. W. Floyd points out, the conditions imply that $|X|≤5$, so the minimum execution time is achieved by referring to a table:

space = 14; time = 4u.
23. The following solution by R. D. Dixon appears to satisfy all the conditions:

24. (a) DIV 3500, where  .
.
(b) SRC 4; SRA 1; SLC 5.
25. Some ideas: (a) Obvious things like faster memory, more input-output devices. (b) The I field could be used for J-register indexing, and/or multiple indexing (to specify two different index registers) and/or “indirect addressing” (exercise 1.4.4–4. (e) A “real time clock” could be added, in a negative memory address. (f) Bitwise operations, jumps on register even or odd, and binary shifts could be added to binary versions of MIX (see, for example, exercises 2.5–28, 5.2.2–12, and 6.3–9; also Program 4.5.2B, 6.4–(24), and Section 7.1). (g) An “execute” command, meaning to perform the instruction at location M, could be another variant of C = 5. (h) Another variant of $\rm C=48,\ldots,55$ could set $\rm CI←register: M$.
26. It is tempting to use a (2:5) field to get at columns 7–10 of the card, but this cannot be done since $2·8+5=21$. To make the program easier to follow, it is presented here in symbolic language, anticipating Section 1.3.2.